document classification 관련 예시 코드는 여기를 확인해주세요.
- Vector space model
- A single document is transformed into a single vector
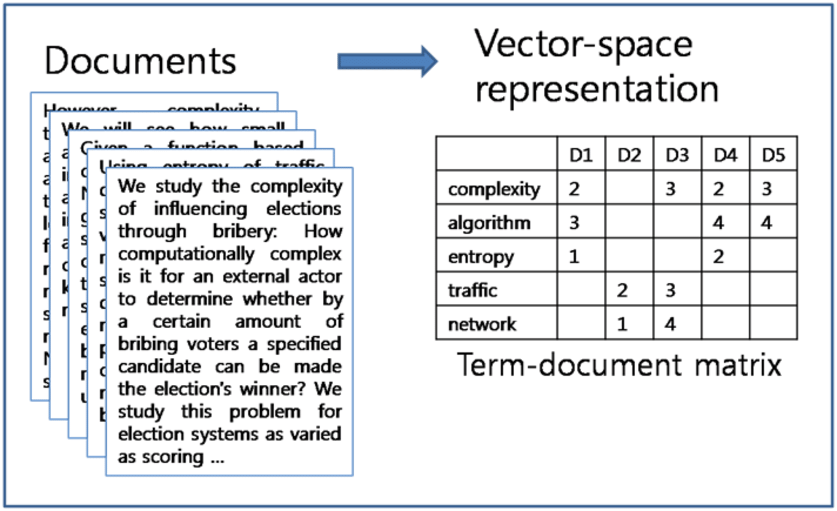
: 각 문서(doc)에서 단어에 대한 p차원(본 그림에서는 5차원)인 vector로 표현하는 것이다.
여기서 자주 사용되는 DTM, Topic Models, Doc2Vec 등이 있습니다.
- Matrix-based Model
- A document is represented as a NxP matrix
▷ N : single doc에서 단어들의 최대 수 (e.g. 512 of BERT)
▷ P : word embedding dimension (e.g. 128)
: 위 그림에서 5차원의 embedding된 vector를 사용하는데, 만약 512차원이 되지 않는다면 padding = 0 을 주어 matrix를 채우게 됩니다.
- Naive Bayesian Classifier

- baye's rule : 통계에서 가장 중요한 rule 중 하나
- naive : 모든 변수들이 통계적으로 독립이라고 가정 한다.
→ 위의 수식에서 마지막 줄처럼 따로 계산을 하게 된다.
- Maximun likelihood estimates
- data에서 간단하게 frequencies를 사용할 수 있다.
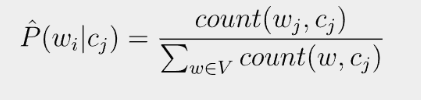
그러나! 문제는
긍정·부정을 구분할 때 (예를 들어)"fantastic"이라는 단어가 한 번도 등장하지 않았다면, 바로 위의 식에서
$w_i = fantastic$으로 분자가 0이 되어버립니다. 즉,$\hat {P} = 0$

① spam인지 아닌지, 즉 positive or negative로 봤을 때, probabilities를 구합니다. (training corpus를 이용해서 계산)
→ 조건부 확률에 대한 곱을 계산합니다.
② smoothing techniques
- Laplace (add-I) : 0이 되는 부분을 방지하기 위해, 분자와 분모에 각 단어의 등장 횟수 +1을 해줍니다.
→ 분자에 0이 되어도(j번 째 범주에 i번째 단어가 등장하지 않았더라도) +1이 되어있고, 분모에는 |vocab| 만큼 더해지게 됩니다.
- k-Nearest Neighbor Classifier : 각 "?"에 해당하는 범주는 어디일까?
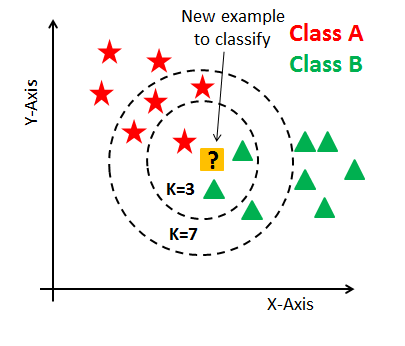
① prepare the referene data
: 새로운 데이터가 들어와야 훈련이 가능하다는 점 (BoW representation or dist. representation)
② define the similarity measure
- 거리와 반비례
- Minkovski distance with order p
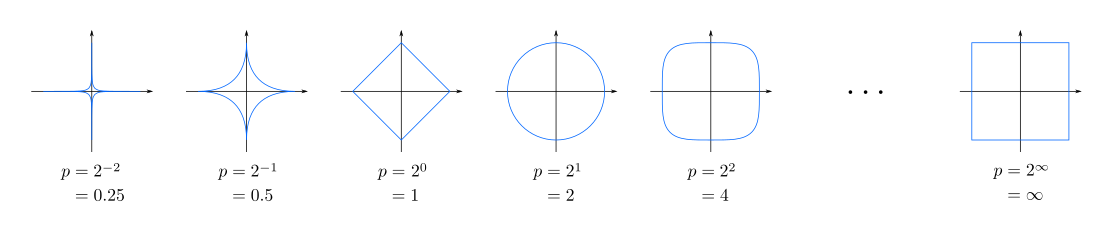
: p = 1, Manhattan distance
p = 2, Euclidian distance와 같다.
③ initialize the set of candidate values for k
- k 가 너무 작으면 overfitting, 너무 크면 underfitting이 되므로 적절한 k를 찾아야 한다.
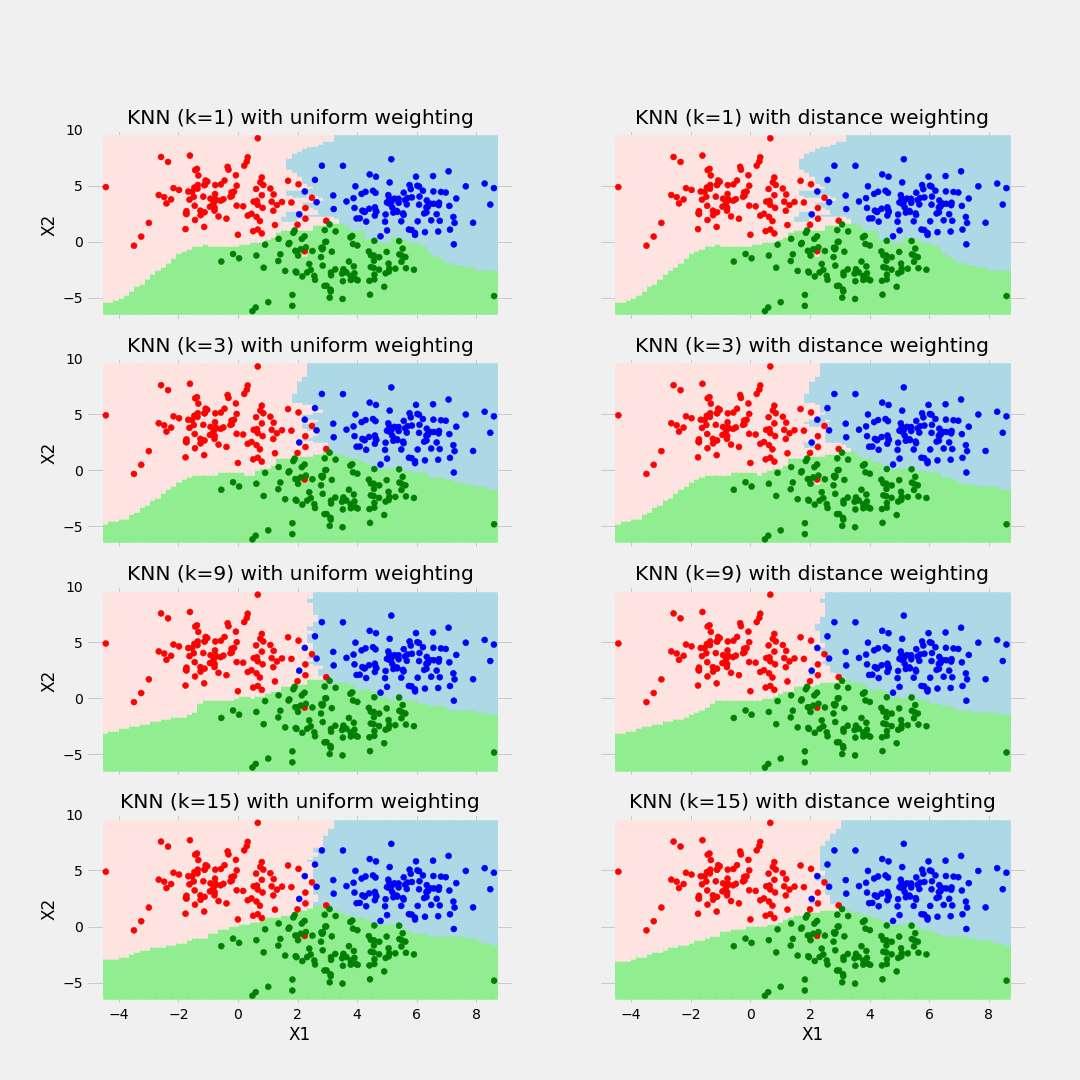
④ determine the combining rule : Majority voting과 Weighted voting 두 가지가 있다.
- Majority voting : 전체 중 해당 class의 비율
- Weighted voting : 더 가까운 distance가 영향력이 더 클 것이므로 distance의 역수를 취해 그 역수의 비율대로 가중치의 합이 1이 되도록 계산한 것.
⑤ 최적의 k를 찾아낸다.
- k-NN issue
1. Normalization
- normalization과 scaling은 k-nn 찾기 전에 끝내야 한다. (두 객체 간의 거리를 계산하는 문제에서는 반드시 한다는 점)
: 측정 지표(단위)가 다르기 때문에 해야 한다.
2. Cut-off
- 각 class의 prior probability를 고려한다.
: 만약 남자가 100명 여자가 400명인 dataset이 있을 때, random 하게 5명을 선택한다. 뽑은 사람이 남성일 기댓값 = 1, 여자일 기댓값 = 4이 된다.
여기서 새로운 X라는 사람에 대해서 비슷한 신체 정보가 비슷한 사람을 5명 뽑을 때 2명은 남성이었다. majority voting = 0.4가 된다. 0.4 < 0.5이므로 기계적으로 이는 여성이다!라고 결론을 내리는 것이 아니라,
prior probability과 비교하므로, (남성일 때 0.2었으므로) 0.4 > 0.2이므로 정보가 주어지지 않았을 때에 비해 정보가 주어졌을 때 남성의 비율이 높아졌으므로 이는 남자이다.
'Deep Learning > Natural Language Processing' 카테고리의 다른 글
| Document Classification (RNN) (0) | 2022.03.28 |
|---|---|
| Document Classification (CNN) (0) | 2022.03.26 |
| [python] 3D 그래프 (0) | 2022.02.10 |
| [python] 데이터 시각화_matplotlib (0) | 2022.02.10 |
| [python]Pandas (0) | 2022.02.09 |