728x90
1. 스토캐스틱 그래디언트 디센트 (Stochastic Gradient Descent) 방법
㉮ 초깃값 설정
㉯ 전체 데이터를 임의로 섞어줍니다.
㉰ 전체 데이터에서 개수가 m개인 부분집합(배치, batch) 들을 만듭니다.
㉱ 각 부분집합마다 다음을 반복합니다.
- 부분집합으로 그래디언트를 계산합니다.
- 계산한 그래디언트의 반대 방향을 탐색 방향으로 설정합니다.
- 주어진 학습률을 그대로 사용합니다.
- 파라미터 추정치를 업데이트합니다.
㉲ 만들어진 부분집합 (=batch) 을 모두 사용한 후 다시 ㉱를 Epoch번 반복합니다.
#SGD
batch_size = 5
Ir = 0.1 #학습률
MaxEpochs = 10 #반복횟수
paths =[]
batch_loss =[]
#1)초깃값
w0 = np.array([4.0,-1.0])
search_direction = np.zeros_like(w0)
#2)데이터 셔플링
np.random.seed(320) #학습 수행 시 섞인 순서 같게 하기 위해(batch 형태 같도록)
idx = np.arange(len(x_train))
np.random.shuffle(idx)
shuffled_x_train = x_train[idx]
shuffled_y_train = y_train[idx]
#알고리즘
for epoch in range(MaxEpochs+1):
for x_batch,y_batch in generate_batches(batch_size, shuffled_x_train,shuffled_y_train): #미니배치생성
paths.append(w0)
batch_loss.append(loss(w0,x_batch,y_batch))
grad = loss_grad(w0, x_batch, y_batch) #미니배치에서 그래디언트 계산
search_direction = -grad #탐색 방향 설정
Ir = Ir #학습률 설정
dw = Ir * search_direction #파라미터 업데이트
w0 = w0 +dw
print('{:02d}\t{}\t {:5.4f}'.format(epoch,w0,loss(w0,x_train,y_train)))
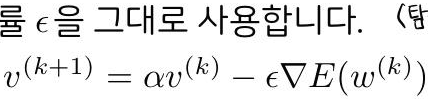
→ update 되어감에 따라 증감이 반복되어가다 결국 감소하게 된다.
2. 모멘텀 (Momentum) 방법
㉮ 초깃값(𝑤0) 설정하고 단기 누적속도 합(𝑣0) = 0으로 초기화 합니다.
㉯ 전체 데이터를 임의로 섞어줍니다.
㉰ 전체 데이터에서 개수가 m개인 부분집합(배치, batch) 들을 만듭니다.
㉱ 각 부분집합마다 다음을 반복합니다.
- 부분집합으로 그래디언트를 현재 위치(𝑤𝑘)에서 계산합니다.
- 주어진 학습률을 그대로 사용합니다. (탐색방향 알고리즘이기 때문)
- 탐색 방향을 아래와 같이 설정합니다.
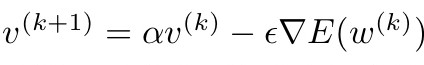
- 파라미터 추정치를 업데이트합니다.
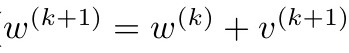
㉲ 만들어진 부분집합 (=batch) 을 모두 사용한 후 다시 ㉱를 Epoch번 반복합니다.
#Momentum
batch_size = 5
epsilon = 0.03 #학습률
MaxEpochs = 10 # 반복횟수
alpha = 0.9
velocity = np.zeros_like(w0)
paths = []
batch_loss = []
w0 = np.array([4.0,-1.0]) #1)초깃값
#2) 데이터 셔플링 전과 동일
#알고리즘
for epoch in range(MaxEpochs+1): #5)MaxEpochs번 반복
#2)미니 배치 생성
for x_batch, y_batch in generate_batches(batch_size,
shuffled_x_train,
shuffled_y_train):
paths.append(w0)
batch_loss.append(loss(w0,x_batch,y_batch))
#4)-1 미니 배치에서 그래디언트 계산
grad = loss_grad(w0,x_batch,y_batch)
epsilon = epsilon #4)-2 학습률 설정
#4)-3 탐색 방향 설정
velocity = alpha * velocity - epsilon*grad #
dw = velocity #4)-4 파라미터 업데이트
w0 = w0+dw
print('{:02d}\t{}\t{:5.4f}'.format(epoch,w0,loss(w0,x_train,y_train)))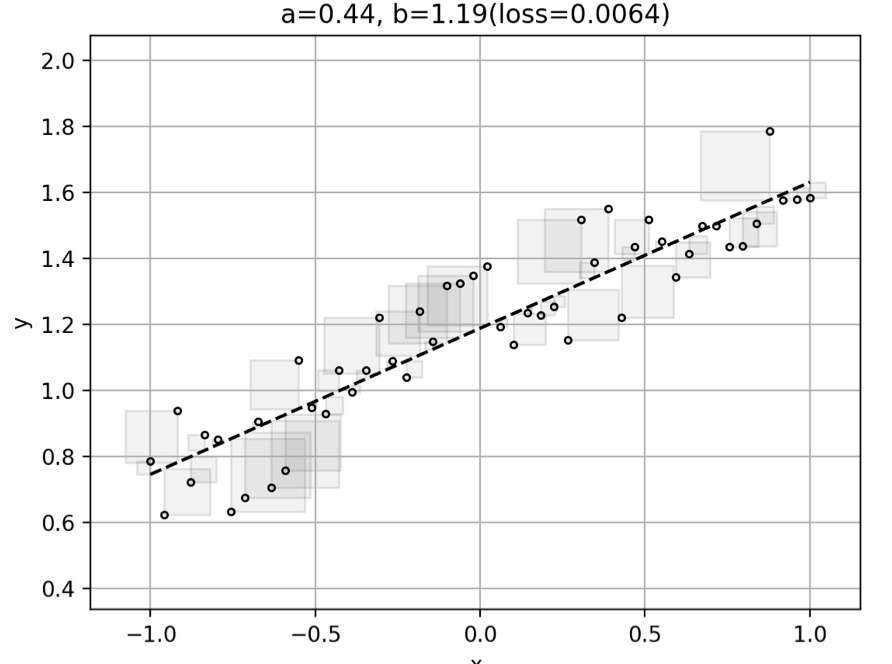
네스테로프 방법은 모멘텀과 비슷한 알고리즘이기에 따로 설명은 덧붙이지 않겠습니다.
728x90
반응형
'Math > Numerical Analysis' 카테고리의 다른 글
| [수치해석] 신경망 모델 (0) | 2022.02.11 |
|---|---|
| [수치해석] Tensorflow 이용 기본 모델 학습 (0) | 2022.02.11 |
| [수치해석] 수치최적화 알고리즘2 (Adagrad, RMSProp, Adam) (0) | 2022.02.11 |