topic modeling 관련 예제는 여기를 확인하세요.
[2012] LDA
- Documents exhibit multiple topics
(배경) 한 document는 여러 개의 topic들이 섞여있을 것이고 (그리고 그게 얼마나 섞여있는지 알아낼 수 있고), 우리는 그런 topic들에서 주로 사용되는 단어가 무엇인지 알아낼 수 있다.
- Each topic is a distribution over words.
- Each document is a mixuture of corpuis-wide topics.
- Each word is drawn from one of those topics.
하지만 실제로 우리는 document자체만 안다. (topic들이 뭔지 모름, 각각의 비중도 모른다는 것이다.)
Q1. Topic의 단어들의 distribution이 뭔가?
Q2. 각각의 topic들의 distribution은?
Q3. 개별 단어들은 어디서부터 추출된 것인가?
→ 이 세 가지를 알아내는 것이 LDA
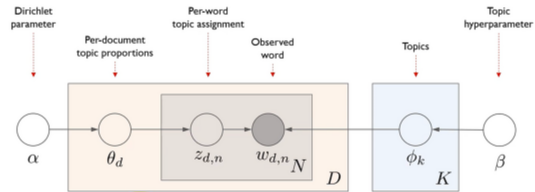
- plate : 반복
- D : 문서
- N : word num
- K : topic num
- α, β : Dirichlet dist.로 부터 나올 hyperparameter
- z_d, n : d번째 문서에서 n번째 단어는 어느 topic에서 추출되는가
- : 각각의 topic들에 대해서 단어들이 얼마 큼의 비중을 가지고 있는지에 대한 dist.
- node는 전부 확률변수 ; edge(α, β)는 θ_d 는 α,

- computing the posterior is intractable (분모를 계산할 수 없다.)
→ approximate algorithms 필요
- Dirichlet Distribution
※ 왜 이 분포여야 했는가?
: binomial & multinomial 관점에서 볼 때,
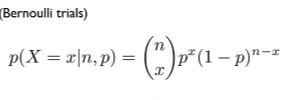
어떤 사건의 outcome이 2가지뿐일 때 (성공/실패로 나눌 때) x번 성공 횟수에 대한 확률 계산을 할 수 있다.
그러나 beta dist. 를 보면

p∈[0,1] : p가 binomial dist. 의 parameter이라 할 때, 우리는 Beta를 "distribution over distribution" (binomial 성공확률 p에 대한 dist.)이라고 생각할 수 있다.
∴ 이 것을 다항 분포로 확장시킨 것이 dirichlet dit.이다.
- Important porperties of Dirichlet distribution
- Posterior is also Dirichlet
- The parameter α controls the mean shape and sparsity of θ
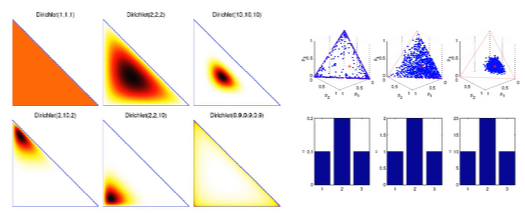
- 첫 그림처럼 dirichlet dist.(1,1,1) = 균등하게 분포되어 있을 것이다.
(그림) (2,2,2)... (10,10,10) 일 수록 더 확신하게 분포되어있을 것이다.
α < 1, 더 극단적인 상황이 만들어짐 (좌측 마지막 그림)

즉, 우리는 실제 관측치 corpus w, hyperparameter α, β 를 이용해
topic assignments z, 문서 단위의 topics의 비중인 θ, topics별 단어들의 가중치인 ϕ를 찾아내는 것이 목적!
- Gibbs Sampling
- Markov Chain Monte Carlo의 형태
- chain은 random variable states의 sequence
- Given a state {z1,... , zk-1} given certain technical conditions, drawing zk ~ p(z1,..., zk-1, zk+1,..., zN | X,θ) for all k (repeatedly) results in a Markov Chain whose stationary distribution is the posterior
- For notational call z with z_d,n removed z_-d, n
나도 이 부분은 처음 듣는 내용이라 이해가 잘 되지 않았다. 쉽게 말하자면,
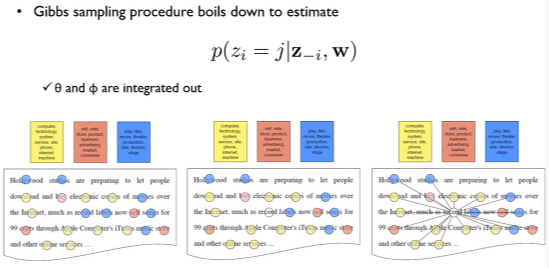
(맨 첫 그림을 보았을 때) w에 대한 topic assignment를 한 것이다.
(두 번째 그림에서) record를 제외하였다고 가정하였을 때 (= z_-i , record 제외 모든 w에 대한 표기 ),
(세 번째 그림처럼) record는 주변 toptic assignment를 가지고 어떤 색, 어떤 topic assignment가 될 것인지를 알아내는 작업이다.
이 sampling이 반복되었을 때, 어느 순간 w들의 색이 변하지 않을 것이다.
[2008][2014] LDA :Inference : Collapsed Gibbs Sampling

- document-topic count : doc에 wi 제외, topic j에 할당된 단어의 수
- document-topic sum : d에 wi 제외 전체 단어의 수
- topic-term count : wi 제외하고 topic j에 할당된 동일한 단어 w의 수 (e.g. 'computer'라는 단어라면, 지금 내가 보는 단어를 빼고 j번째 할당된 게 몇 개인가)
- topic-term sum : wi 제외하고 j번째 topic 할당된 전체 단어의 수
를 뜻한다.
'Lecture Review > DSBA' 카테고리의 다른 글
| [2017] Transformer : Attention Is All You Need (0) | 2022.03.17 |
|---|---|
| [2014] Seq2Seq Learning with Neural Networks (0) | 2022.03.16 |
| Topic Modeling - 1 (0) | 2022.03.08 |
| Dimensionality Reduction (2) | 2022.03.04 |
| Doc2Vec & Others (0) | 2022.03.02 |