- 퍼셉트론 : 가장 간단한 신경망
$y = f(w * x + b)$
- 선형 함수와 비선형 함수의 조합으로 선형 함수 표현인 $wx + b$ 는 아핀 변환 (affine transform)이라고도 한다.
2. 활성화 함수
(1) 시그모이드
$f(x) = \frac{1}{1+e^{-x}}$

- 입력 범위 대부분에서 매우 빠르게 포화되어 gradient가 0이 되거나 발산하여 부동소수 오버플로가 되는 문제 발생.
→ 그레이디언트 소실/ 폭주 문제
→ 신경망에서 거의 출력층에서만 쓰임
(2) 하이퍼볼릭 탄젠트
$f(x) = tanh x = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

- (-∞,∞) 범위의 실숫값을 [-1, 1]로 바꾼다.
(3) 렐루
$f(x) = max(0, x)$
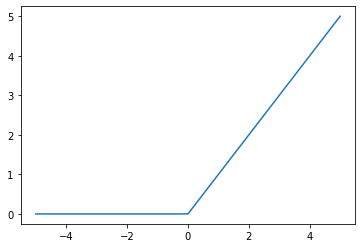
- gradient vanishing problem에 도움이 된다.
- 시간이 지나면 신경망의 특정 출력이 0이 되면서 다시 돌아오지 않는 문제 발생
(3) - 1. PReLU
$f(x) = max(x, ax)$
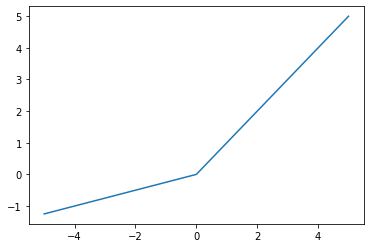
- 죽은 렐루 문제 줄이기 위해 쓰이는 활성화 함수.
- 리키 렐루 (Leaky ReLU)도 쓰임
(4) 소프트맥스
$softmax(x_i) = \frac{e^{x_i}}{\sum_{f=1}^k e^{x_f}}$
- 모든 출력의 합으로 각 출력을 나누어 k개 클래스에 대한 이산 확률 분포를 만든다.
- 소프트맥스 출력의 합은 1
- 분류 작업의 출력을 해석하는데 유용하다.
- 보통 objective function인 cross entropy와 함께 사용
3. 손실 함수
(1) 평균 제곱 오차 손실
$L_{MSE}(y, \hat{y}) = \frac{1}{n} \sum_{i=1}^n (y-\hat{y})^2$
- 예측과 타깃값의 차이를 제곱하여 평균한 (실숫)값.
(2) 범주형 크로스 엔트로피 손실
$L_{cross-entropy} (y, \hat{y}) = - \sum_{i} y_i log(\hat{y_i})$
- 출력 클래스 소속 확률에 대한 예측
- 정답 클래스의 확률은 1에 가깝고 다른 클래스의 확률은 0에 가까운 상태가 바람직하다.
(3) 이진 크로스 엔트로피 손실
- 두 개의 클래스로 분류하는 이진 분류
- 신경망 출력을 가장한 랜덤 벡터에 시그모이드 활성화 함수를 적용해 이진 확률 벡터인 probabilities를 만든다,
- 그 후 정답 targets를 0과 1로 이루어진 벡터로 만든다.
- 위 둘을 사용하여 binary cross entropy loss 구한다.
'Deep Learning > Natural Language Processing' 카테고리의 다른 글
| [pytorch] 단어와 타입 임베딩 (2) | 2022.07.27 |
|---|---|
| [pytorch] Feed-forward network (0) | 2022.07.25 |
| [pytorch] nlp기술 빠르게 훑어보기 (0) | 2022.07.18 |
| [pytorch] Intro (0) | 2022.07.18 |
| 감성 분석 Sentiment Analysis (0) | 2022.03.29 |