[2017] Neural Collaborative Filtering
Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, Tat-Seng Chua
본문의 논문은 ICER paper로, 링크를 확인해 주세요.
Introduction
추천 시스템은 이전에도 궁금하여 다루어 보았던 내용으로, collaborative filtering기법에서 가장 대표적으로 많이 사용되는 matrix factorization (MF)이 있다. 이는 유저 또는 아이템의 잠재적 특성을 가진 벡터를 사용하여 곱하여 계산하는 방식이다. 즉, 아이템에 대한 사용자의 상호작용을 내적을 이용하여 모델링한 것이다.
추천 시스템에 적용되는 가장 유명한 것으로 넷플릭스를 뽑을 수 있다. 이는 유저의 시청 기록을 바탕으로, 다른 사람의 시청과 비교하여 비슷한 영화를 보았을 때 추천해 주는 방식이다. 여기에도 MF가 사용되는 것이다.
저자들은 MF에 DNN을 적용한 방식을 본 논문에서 보여주며, main contributions는 다음과 같다.
1. 유저와 아이템의 잠재적 특성을 NN에 적용하고, 일반적인 NCF 형태에 NN 기반의 collaborative filtering을 고안하였다.
2. MF가 NCF의 특별함을 보일 수 있고, 다중 퍼셉트론을 활용하여 높은 수준의 비선형성의 NCF 모델링을 보여준다.
3. 저자들의 NCF의 효율성과 collaborative filtering에 대한 딥러닝의 보증을 실험을 통해 보여준다.
Preliminaries
Learning from Implcit Data
M과 N은 각각 유저와 아이템의 수이고, 유저와 아이템의 상호 matrix를 $\mathbf{Y} ∈ \mathbb{R}^{M \times N}$이라 할 때, 다음을 따른다.
$y_{ui} = \begin{cases} 1, & \mbox{if }\mbox{ interaction (user $u$, item $i$) is observed;} \\ 0, & \mbox{}\mbox{otherwise.} \end{cases}$
1이라고 해서 유저가 아이템을 좋아하는 것도 아니고, 0이라고 해서 유저가 아이템을 싫어하는 것이 아니며, 그저 아이템을 인식하지 못했다고 볼 수 있다. 그래서 암시적인 데이터에 대해서는 꽤나 어려운 예측이 될 것이다.
일반적으로 추정된 데이터 $\hat{y}_{ui} = f(u,i| \theta)$는 $y_{ui}$의 예측 점수이며, $\theta$는 파라미터, $f$는 모델의 예측 점수 (interaction funciton으로 언급)이다.
파라미터인 $\theta$의 추정치는 일반적으로 기계학습의 objective funciton의 최적화 값의 패러다임을 따르는데, 여기서 대표적으로 pointwise loss와 pairwise loss를 사용한다.
pointwise 학습 방법은 $y_{ui}$와 $\hat{y}_{ui}$의 loss 제곱 값이 최소가 되는 값을 가지는 것이다. 부정 데이터가 없을 때, 모든 관측되지 않은 entries (negative feedback)이나 관측되지 않은 entries에서 샘플링한 instances로 다루게 된다.
pairwise 학습 방법은 관측 데이터는 비관측 데이터에 비해 높은 순위를 가지게 된다. 관측치 $y_{ui}$와 비관측치$\hat{y}_{ui}$ 사이의 마진을 최대화하여 학습한다.
Matrix Fatorization
$\mathbf{p}_u$와 $\mathbf{q}_i$는 각각 유저와 아이템에 대한 latent vector로 표현할 때, MF는 이 둘의 내적곱을 이용하여 다음 $y_{ui}$ 값을 가진다.
$\hat{y}_{ui} = f(u,i|\mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}^T_u \mathbf{q}_i = \sum^K_{k=1} p_{uk}q_{ik}$
여기서 K는 latent space의 차원 값이다.
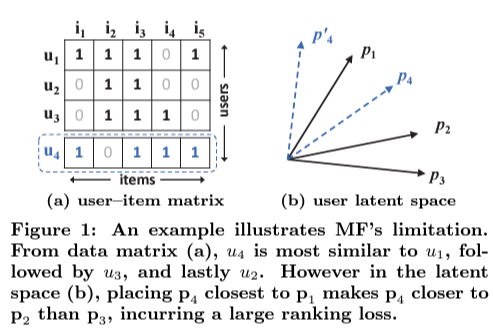
위 그림에서 보면, MF은 유저와 아이템을 같은 latent space에 매핑하므로, 두 유저 간의 유사도를 latent 벡터 간의 코사인 값으로 내적곱 또는 동일하게 (latent vectors는 길이의 단위로 가정한다.) 측정될 수 있다. 두 번째로, 일반적인 loss 없이 Jaccard 유사도를 ground truth로 사용한다.
figure(a)에서 $u_4$와 가장 가까운 순을 보았을 때, $u_1, u_3, u_2$로 볼 것이다. 이를 바탕으로 (b)의 벡터 공간에서의 보면, $\mathbf{p}_4$는 $\mathbf{p}_1$과 가장 가깝고 그 다음으로, $\mathbf{p}_2$, $\mathbf{p}_3$이 됨을 알 수 있다. 바로 이 부분이 MF의 한계점으로 볼 수 있는 것이다.
이를 해결하기 위해 latent factor 인 $K$를 더 크게 (추가) 한다면, overfitting과 같은 문제를 야기할 수 있게 된다. 그리하여 저자들은 이런 데이터를 위해 DNN을 결합하였다.
Neural Collaborative Filtering
General Framework w/ Generalized Matrix Factorization (GMF)
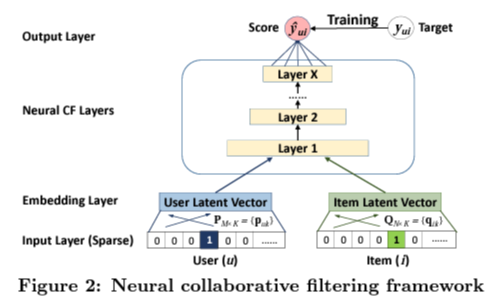
· input data에서 유저 또는 아이템은 one-hot encoding하여 얻어진 벡터는 각각의 latent 벡터
· $\phi_1(\mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_u ⊙ \mathbf{q}_i$, 여기서 ⊙은 성분곱
· 이를 통해 neural CF layer를 겹겹이 쌓아 올려 output을 가지게 된다.
· $\hat{y}_{ui} = a_{out}(\mathbf{h}^T(\mathbf{p}_u ⊙ \mathbf{q}_i))$
· $a_{out}, \mathbf{h}$는 각각 non-linear activation funciton (sigmoid)과 output layer의 edge weights
Multi-Layer Perceptrion (MLP)
NCF framework 아래에 MLP 모델을 다음과 같이 정의하여 연산한다.
$\mathbf{z}_1 = \phi(\mathbf{p}_u,\mathbf{q}_i) = \left [\mathbf{p}_u \over \mathbf{q}_i \right]$,
$\phi_2(\mathbf{z}_1) = a_2(\mathbf{W}^T_2 \mathbf{z}_1 + \mathbf{b}_2)$,
.....
$\phi_L(\mathbf{z}_{L-1}) = a_L(\mathbf{W}^T_L \mathbf{z}_{L-1} + \mathbf{b}_L)$,
$\hat{y}_{ui} = \sigma(\mathbf{h}^T \phi_L(\mathbf{z}_{L-1}))$
$\mathbf{W}_x, \mathbf{b}_x. a_x$는 각각 weight matrix, bias vector, activation function이다.
Fusion of GMF and MLP

GMF와 MLP를 혼합하기 위해서는 이 둘이 같은 embedding layer를 공유해야 한다. 하지만 이 둘의 혼합은 성능 부분에서 제약이 있을 수 있다. 그렇기 때문에 embedding은 따로 하되, 두 모델의 마지막 hidden layer를 concate 하는 방법을 사용하였다.
$\phi^{GMF} = \mathbf{p}^G_u ⊙ \mathbf{q}^G_i$,
$\phi^{MLP} = a_L(\mathbf{W}^T_L(a_{L-1}(... a_2(\mathbf{W}^T_2 \left [\mathbf{p}^M_u \over \mathbf{q}^M_i \right] + \mathbf{b}_2)...)) + \mathbf{b}_L)$,
$\hat{y}_{ui} = \sigma(\mathbf{h}^T \left [\phi^{GMF} \over \phi^{MLP} \right] )$
여기서 $\mathbf{p}^G_u, \mathbf{p}^M_u$ 은 각각 GMF와 MLP를 위한 유저 embedding 부분이며, $\mathbf{q}^G_i, \mathbf{q}^M_i$ 또한 아이템의 GMF와 MLP를 뜻한다.
NCF loss function
- likelihood function
$p(\mathcal{Y,Y^-} | \mathcal{P,Q}, \theta_f) = \prod_{(u,i)∈ \mathcal{Y}} \hat{y}_{ui} \prod_{(u,j)∈ \mathcal{Y}^-} (1-\hat{y}_{uj})$
- SGD 수행에 있어 최적화를 위한 binary cross entropy
$L = - \sum_{(u,i)∈ \mathcal{Y}} log \hat{y}_{ui} - \sum_{(u,j)∈ \mathcal{Y}^-} log (1 - \hat{y}_{uj})$
$ = -\sum_{(u,i)∈ \mathcal{Y}∪\mathcal{Y}-} y_{ui} log \hat{y}_{ui} + (1 - y_{ui}) log(1 - \hat{y}_{ui})$
Experiment
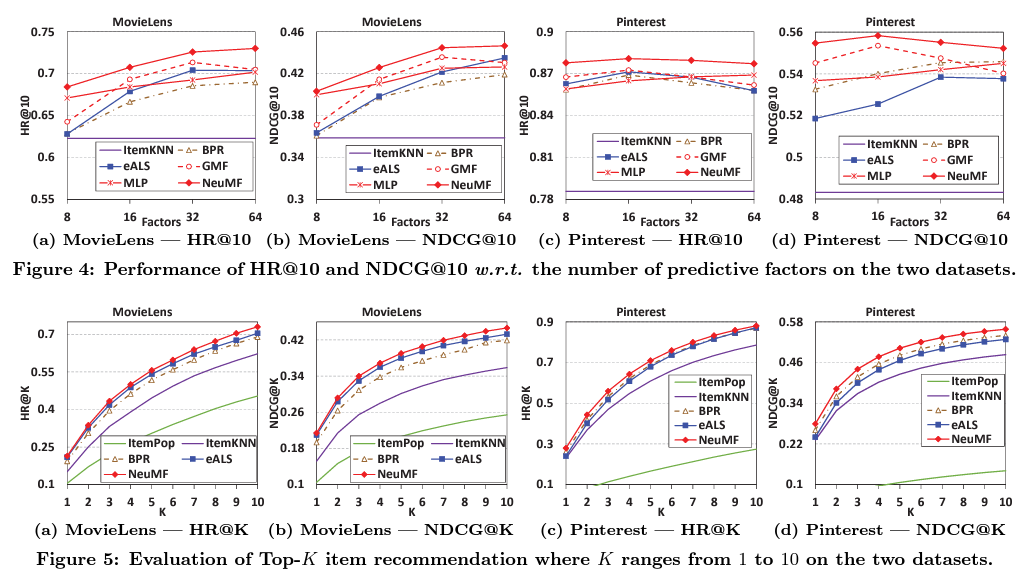
Pretraining 성능 차이
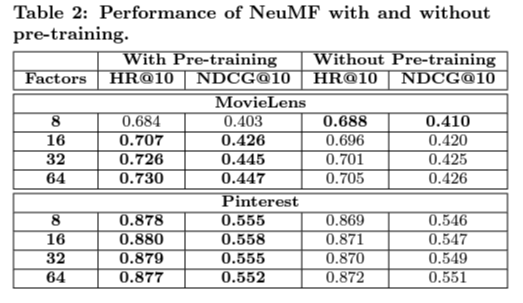
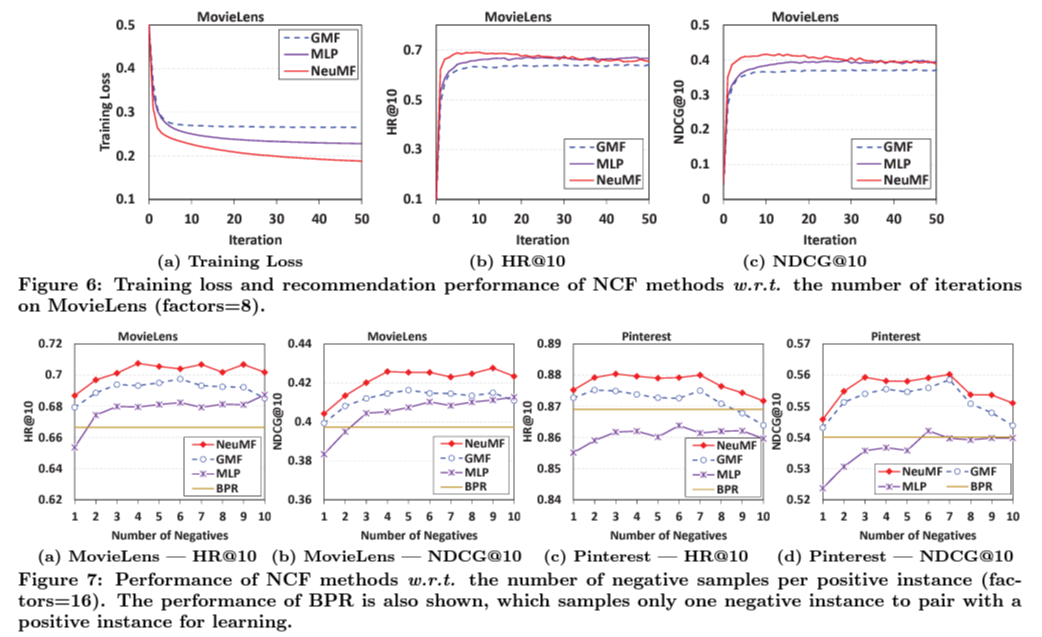
Training loss and total performance
용어 정리
1. pointwise train
: 간단히 말해 한 번에 하나의 (point) 아이템 고려.
한 개의 입력 데이터에 대해 예측 값과 정답 값에 대한 차이만 계산
(한계점)
item - item 간의 관계를 학습에 반영하지 못함. (ex. A보다 B가 좋다.)
top-N을 inference 결과로 가져오게 된다.
2. pairwise train
: 한 번에 두 개의 아이템을 고려하여 비교.
pos / neg 하나씩 각각 고려하기 때문에 아이템 간의 관계로 (선호 관계) 순위를 정할 수 있다.
(한계점)
연산량이 많아진다.