추천 시스템에서 기반이 되는 Factorization 에 대해 간략히 정리하고자 한다.
MF (Matrix Factorizatoin)
Matrix Factorization은 가장 대중적인 Latent Factor model로, SVD(Singular Value Decomposition)과 유사하게 유저와 아이템을 $f$차원의 latent factor space로 매핑한다.
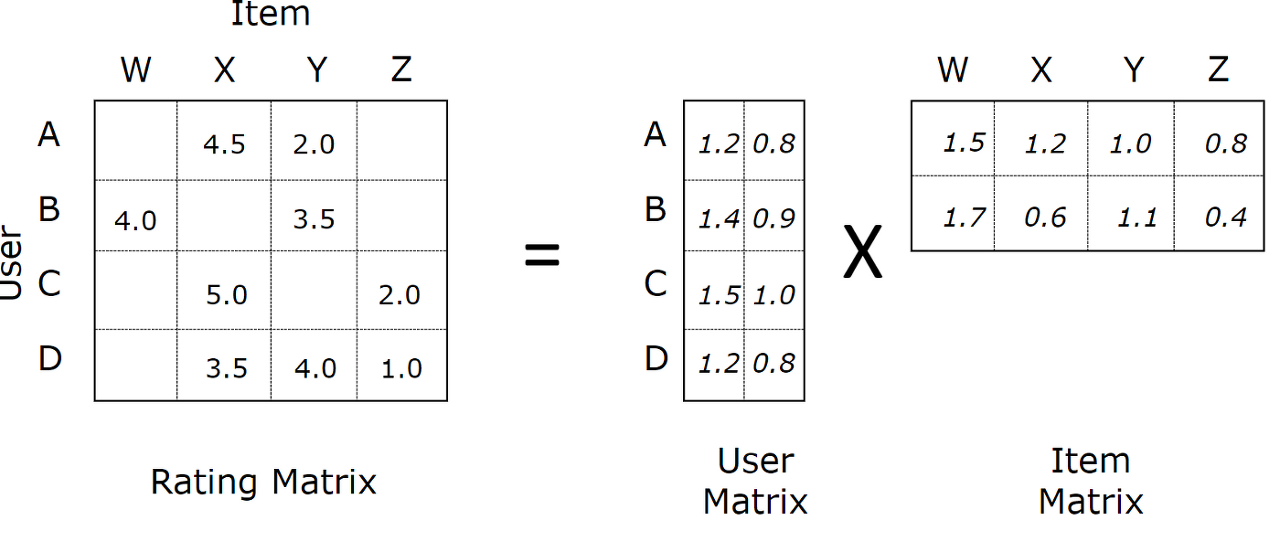
$f$개의 latent factor 로 표현된 user, item vector $\mathbf{p}_u, \mathbf{q}_i$의 내적으로 둘 사이의 interaction $\hat{\mathbf{r}}_{ui}$를 다음과 같이 구한다.
$\hat{\mathbf{r}}_{ui} = \mathbf{p}_u \mathbf{q}_i$
Factorization Machine
MF는 SVM과는 반대로 일반적인 데이터에 바로 적용할 수 없으므로, 대부분의 경우 task specific한 model이라는 단점이 있다.
FM은 SVM과 MF의 장점을 함께 가진 모델로, 다음과 같은 장점이 있다.
· Sparse data : SVM으로 학습하기 어려운 sparse한 환경에서도 parameter 추정이 가능.
· Linear Complexity : SVM과 같은 쌍대문제 (duality problem)를 해결하지 않아도 된다.
※ duality problem : linear 상황에서 optimum을 찾을 때, 최적값을 찾게 된다면 그에 대한 검증이 필요. 어떤 최적값에 대한 하한, 상항으로 검증하는 방법.
· General Predictor : General predictor로서 어떠한 실수 벡터를 사용하더라도 잘 작동한다.

2-way FM
$\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^n w_ix_i + \sum_{i=1}^n \sum_{j=i+1}^n <\mathbf{v}_i , \mathbf{v}_j> x_ix_j$
- $w_0$ 는 $\mathbb{R]$차원의 global bias
- $w_i$ 는 개별 features에 대한 weight
- $<\mathbf{v}_i, \mathbf{v}_j>$는 f개의 latent factor로 표현된 변수 간의 2-way interaction을 계산하는 내적을 의미
Computation

linear complexity 특성으로 인해 n-way 환경에서도 연산량이 줄어듦을 볼 수 있다.
d-way FM
$\hat{y}(x) := w_0 + \sum_{i=1}^n w_ix_i + \sum_{l=2}^d \sum_{i_1=1}^n \cdots \sum_{i_l=i_{l-1}+1}^n ( \prod_{j=1}^l x_{i_j})(\sum_{f=1}^{k_l} \prod_{j=1}^l v_{{i_j},f}^{(l)})$

