[2022] On Curriculum Learning for Commonsense Reasoning

 

[2022] On Curriculum Learning for Commonsense Reasoning

Adyasha Maharana    Mohit Bansal

 

본문의 논문은 NAACL 2022 Accepted paper로, 여기를 확인해주세요.

 

 

 

Abstract

 

 상식 추론은 target task 데이터에서 pre-trained 언어 모델을 fine-tuning 하는 표준 패러다임을 따르며, 여기서 훈련 중에 샘플이 랜덤한 순서로 모델에 들어간다. 하지만 최근 연구에서는 데이터의 순서가 자연어 이해를 위한 fin-tuned 모델의 성능에 중요한 영향을 준다고 한다. 그러므로 상식 추론에서 언어 모델의 fine-tuning 동안 인간 같은 어려워지는 난이도 커리큘럼의 효과를 설명한다. 속도가 pacing 커리큘럼 학습을 사용하여 데이터의 순위를 매기고, fine-tuning 동안 순위가 매겨진 데이터셋에서 난이도가 증가한 미니 배치를 샘플링하였다. 게다가 적응적인 커리큘럼의 효과를 조사하였는데 즉, 순위 데이터가 학습자 모델의 현재 상태를 기반으로 훈련 동안 동적으로 순위를 업데이트된다. 저자들은 각 샘플의 난이도를 측정하고 질의응답, 변동성과 분포 이탈을 기반한 세 가지 척도로 실험하였다. 다양한 방법에서 커리큘럼 학습의 효과를 이해하기 위해 파라미터의 효과적인 prompt-tuning뿐만 아니라 전체 모델 fine-tuning에도 적용한다. 

 

 

 

 Introduction

 

 

 커리큘럼 학습은 1993년에 제안한 논문에서 나온 단어로, 훈련 데이터의 전형적인 uniform 랜덤 샘플링의 대안책으로, 일반적으로 사람이 초급 수준의 학습부터 대학 수준의 학습 내용까지 긴 기간을 가지고 학습하는 것을 의미하는데, 이를 머신러닝에 적용한 것이다. 처음엔 쉬운 샘플만 보여주다가 점차 어려운 샘플을 보여주는 것이다. 머신러닝 패러다임에서, ' teacher '는 훈련 샘플을 쉬운 것에서 어려운 순서로 순위를 매기고, 그 순서대로 ' learner '에게 보여준다. Dodge et al.은 랜덤 하게 초기화한 훈련 데이터의 순서가 모델의 성능에 큰 다양성을 이끎을 보여주었다. 이런 증거들에 근거하여, 저자들은 "데이터셋 분포나 모델의 신뢰도에 기반한 커리큘럼 같은 의미 있는 데이터의 순서가 랜덤 데이터 순서에도 능가하는 성능을 보일까?" 에 대한 답을 한다. 그런 실험들은 기계 번역과 자연어 이해 같은 NLP에서 긍정적인 성능을 보여온  반면에 large pretrained models (PTMLs)는 이런 작업에서 높은 성능을 보였지만, 상식 추론 능력에 제한되었다. 게다가 인간의 상식 습득의 과정은 기계에서 동일한 것을 달성하기 위한 알고리즘을 개발하는 데 유용하였다. 그러므로 저자들은 상식 추론에서 PTMLs의 funetuning을 향상시키기 위해 인간 같은 커리큘럼 학습의 효과에 대해 연구하였다.

샘플링 훈련 미니 배치를 위한 데이터 순서에 구조를 적용하기 위해, transfer에 의한 pacing 커리큘럼 학습을 선택하여야 한다. 이 방법은 pacing 함수가 모델이 훈련 동안에 순위화 된 데이터를 나타내는 속도를 결정하는데 도움이 된다. 훈련 데이터 셋의 순위는 랜덤 훈련 순서를 사용하여 target 데이터 셋에서 finetuned 한 pretrained network의 출력을 사용하여 수행한다. 이런 접근을 고정된 커리큘럼 학습이라고 한다. 인간이 스킬 셋을 습득하는 동안, student은 student의 학습 과정에 따라 교사에 의해 계속해서 조정되는 커리큘럼의 혜택을 받을 수 있다.

또한 상식 추론을 위한 적응형 커리큘럼 학습을 조사한다. teacher model에 의해 도입된 초기 데이터 순서는 learner model의 현재 상태를 고려하여 훈련 중에 정기적으로 업데이트된다. 중요한 것은, 일반화에 이점이 되는 것으로 나타난 학습하기 어려운 데이터 포인트의 피드백을 강화하기 위해 ACL에서 난이도를 쉽게 바꿀 수 있는 커리큘럼으로 순위를 되돌릴 것을 제안한다. 난이도 측정을 위해 question answering probability(QAP), Energy-Based Out-of-Distribution, Cartography, 이 세 가지 다른 데이터 샘플 정보 점수 방법을 분석한다. 저자들의 연구는 훈련 데이터를 N개의 meta 데이터셋으로 나누고, 커리큘럼 계산을 위해 N 모델을 훈련하고 휴리스틱 하게 설계된 방법을 따르는 Xu et al. 와 가장 연관 있다. 그와 반대로 저자들은 커리큘럼 연산을 위해 단일 모델을 훈련하였고, 베이지안 최적화를 사용하여 target 데이터셋에 대한 커리큘럼의 최상의 pacing을 찾았다. 이는 Xu보다 효과적이다.

 

 

 

 

 Related Work

 

 Curriculum learning (CL) 은 강화 학습과 neural machine translation에서 많이 쓰이고 있고, 질문 생성, 정보 검색, 자연어 이해 그리고 개체 인식 각 부분에서 효과를 입증하였다. 저자들은 상식 추론을 위한 CL의 효과를 처음 입증하였다. 

 task 별 sample 복잡성의 다양한 측정은 이전부터 많이 연구되어 왔다. 예를 들어, 자연어 추론을 위한 inter-annotator agreement, 추상적 의미 표현(AMR)을 위한 sub-graph의 깊이 구조, jittering (순간적 흐트러짐으로 이해하면 될 듯) 기반 데이터 증강 PCA에서 noise의 비율, 일련의 모델링을 위한 문장 길이, 감성 분석을 위한 의미론적 유사성 등이 있다. Wang et al.은 그래프 분류 task를 위한 그래프 임베딩 분포를 모델링하는 neural density 추정기를 사용하였다. 저자들은 난이도를 계산하기 위해 pretrained model 기반 점수를 사용했다.

 그 후 다른 논문에서 adaptive 커리큘럼이 이미지 분류와 neural 반응 생성에서도 좋은 성능을 냄을 보여주었다. 그리고 저자들은 CL을 이용한 상식 추론을 보일 것이다.

 

 

 

 

 Methods

 

 

1. Curriculum Learning

 

  커리큘럼 학습은 두 가지의 다른 성질이 있다. 즉, 난이도에 따른 순위 매기기와 훈련 동안 샘플을 쉬운 것에서 어려운 것으로 전이하는 것이다. transfer 방법에 따르면, 저자들은 난이도에 의해 기존 샘플뿐만 아니라 종합적인 것도 순위를 매기기 위해 target 데이터 셋에 훈련된 모델(CL 없이) 의 예측을 사용한다. 이는 위 그림을 참고하면 된다. 저자들은 쉬운 예제에서 어려운 것으로 전이하는 것을 시행하기 위해  fixed pacing 함수를 적용하고, 베이지안 최적화를 사용한 pacing 함수의 하이퍼파라미터를 최적화한다.

 pacing 함수 $p_f(i)$는 미니배치인 ${B_i}$ 가 훈련 동안에 uniform하게 샘플링되는 $|X_i| = p_f{i} * |X|$ 크기의 subset $X_1, ... , X_m ⊆ X$ sequence를 결정하는 데 사용된다. 여기서 $X$는 순위화 된 훈련 데이터 셋이다. fixed pacing function은 세 개의 파라미터로 구성되는데, 1) 시작 백분율 2) 요인 증가, 3) step length이다. 커리큘럼 학습의 각 스텝에서 훈련 iteration의 값은 step length로 정의된다. 1) 시작 백분율은 첫 커리큘럼 학습 단계에서 모델에 반영된 훈련 샘플의 최대 난이도를 결정한다. 2)요인 증가는 각 단계의 마지막에 최대 난이도를 기하급수적으로 확장하는 데 사용된다. 백분율은 $p_f(i) = t * \gamma^{[i/S}$로 계산되고, 여기서 $t , \gamma , S, i$는 각각 시작 백분율, 요인 증가, step length, 현재 훈련 iteration이다. 훈련은 순위화 된 데이터셋의 $t$%를 샘플링하여 초기화하고, 사용 퍼센트는 모든  $S$ iteration의 마지막에서 다시 계산한다.

 

 

 

2. Adaptive Curriculum Learning

 

 student를 위한 최적의 커리큘럼이 미리 알려지지 않았을 때, teacher은 과거의 teaching 경험에 기반한 커리큘럼을 세우고, student의 학습 과정에 조정한다.  Kong et al.에 따르면, 난이도 점수를 얻은 teacher model을 사용한 초기화 커리큘럼을 제안하였고, 그 점수를 학습자 모델의 현 상태에 적용한다. 훈련 동안에 점수는 모든 $L$ 최적화 단계마다 업데이트된다. ($k$+1)번째 업데이트 때, 난이도 점수는 다음과 같이 계산된다. 

 

 여기서 $\mu_{cur}, \mu_k, \mu_{k+1}$은 현 단계 이후 난이도 점수, $k$번째와 ($k$+1) 번째 업데이트이다. $\alpha 와 L$은 tunable 하이퍼 파라미터이다. 순위는 어려운 샘플을 최대화하기 위해 subsequent 훈련 동안 업데이트된 점수를 사용한 flipped to a difficult-to-easy 방법이다.

 

 

 

3. Difficulty Scoring Functions

 

• Question Answering Probability (QAP)

 teacher model이 적확하게 질문에 대한 답을 할 수 있는 확률은 특정 데이터 샘플에 대한 모델의 신뢰도를 측정하는 것이다.이 metric을 순위 데이터셋에 사용하였는데, 높은 QAP를 가진 데이터 샘플은 쉬운 것으로, 낮은 QAP를 가진 데이터 샘플은 어려운 것으로 다루었다. 여기서 질의응답 쌍인 $(x_i, y^*_i)$에 대한 QAP $\mu_i$는 $p_{\theta}(y^*_i|x_i)$로 측정한다.

 

• Model Variability

  Swayamdipta et al.은 데이터 샘플이 모델의 일반화 오류에 미치는 영향을 식별하기 위한 모델의 신뢰도 $(\hat{\mu_i})$와 다양성 $(\hat{sigma_i})$ 측정을 제안하였다. 여기서 각각은 다음 식으로 계산되고, E는 훈련 epoch의 수이다.

model confidence

variability

 

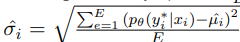
 저자들은 샘플을 다양성의 오름차순으로 순위를 매겼다. 쉽게 말하면, 낮은 다양성을 가진 샘플은 쉬움으로 순위를 매긴 것이다.

 

• Energy

 Liu et al은 에너지 점수가 in- and out-of distribution(OOD)의 사이에 특징을 확실하게 구분하는데 사용했다. 저자들은 자신의 커리큘럼에서 이 metric을 OOD 샘플을 어려움으로 , in-of-distribution을 쉬움으로 순위를 매겼다. 주어진 샘플의 에너지는 다음과 같이 계산하였고, 여기서 $f_i(x)$는 주어진 샘플의 logit으로 teacher model에서 가져온 것이고, $T$는 temperature이다.

 

 

 

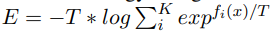
▶ 참고로 logit은 오즈에 자연로그를 씌운 것으로, log + odds로 보면 된다. 오즈는 그 값이 1보다 큰지 결정의 기준이고, 로짓은 0보다 큰지가 결정의 기준이다.

 

 

 

 

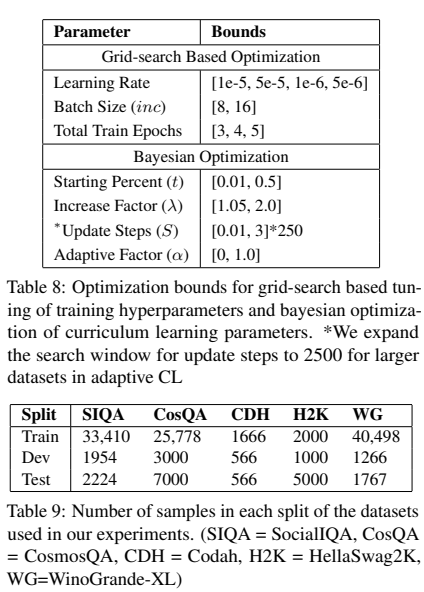
 Experimental Setup

 

 

 $RoBERTa_{Large}$를 learner model 뿐만 아니라 teacher 로써도 사용하였다. 처음에 teacher model은 랜덤 하게 샘플링한 훈련 데이터에서 funetuned 하고 난이도 점수를 계산하는 데 사용했다. 모델은 필요하면 첫 단계에서 훈련 하이퍼파라미터의 grid-search 기반 튜닝을 사용하였다. 두 번째에서는 adaptive CL 뿐만 아니라 fixed에 대한 최적의 pacing function 파라미터를 찾기 위해 베이지안 최적화를 사용한다. 그리고 첫 번째와 같이 같은 훈련 파라미터를 사용한다. adaptive learning에서, $L = S$로 설정하고, $\alpha , t, \gamma, S$는 최적화하였다. prefix tuning 실험에서, $GPT2_{LARGE}$를 튜닝을 위한 PTML로 사용하였다.

 

 

 

 

 Results & Analysis

 

 1. Main Results

 

 teacher model에 초기화 순위는 첫 S 훈련 스텝 후에 그렇게 유용하지 않았기에, 최적의 $\alpha$는 1.0에 가깝게 실험하였다.

 

 

 

 

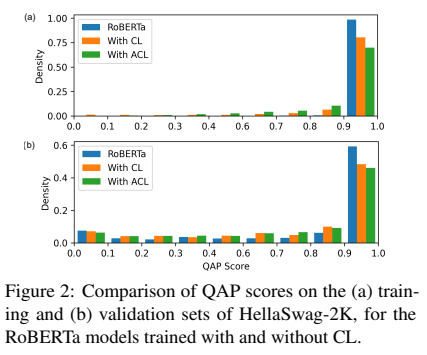
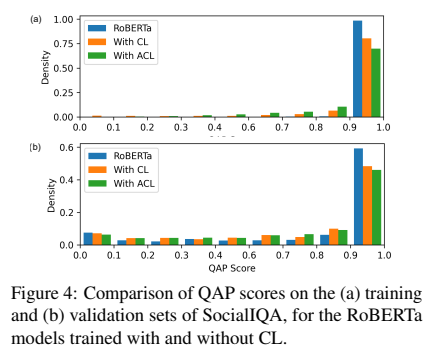
 커리큘럼 학습의 효과를 보이기 위해, 저자들은 teacher vs. learner models를 위해 난이도 스코어를 training과 validation sets을 비교하였다. 저자들은 learner model이 덜 overfitting한 것을 암시함을 training data에 대해 덜 신뢰한다는 것을 보여준다. 이는 validation set에서 보이지 않는 데이터에 대한 일반화를 개선하고, 샘플에 대한 QAP 점수의 더 균일한 분포를 초래한다.

 

 

 

2. Difficulty Metrics

QAP에서 가장 좋은 성능을 보임

 

 

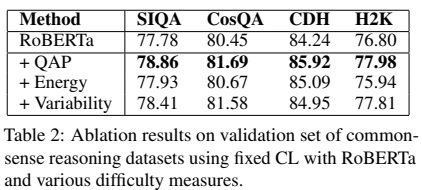
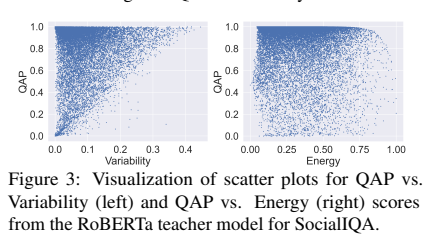
  높은 QAP를 가진 샘플은 낮은 분산을 보임을 나타내고 있고, 이 두 metric이 커리큘럼 학습에서 비슷한 행동을 이끈다고 할 수 있다.

 

 

 

3. Curriculum Learning for Prefix-Tuning

 

 

 

 

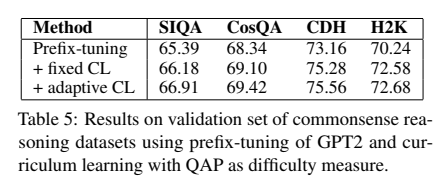
4. Curriculum Learning for Natural Language Understanding

 

 

 

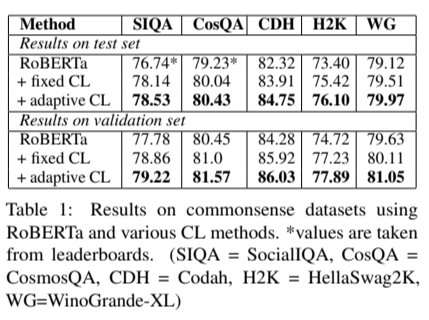
 작은 GLUE 데이터셋에 대해, 커리큘럼 학습 접근 방식은 작은 margin 향상을 보였다. 그에 반해 작은 상식 추론 데이터셋에 대해 큰 향상을 보여주었다.

 

 

 

 

 Limitations

 

 저자들의 방식은 상식 추론과 자연어 이해에 기반한 객관적인 다중 선택 질의응답 task에 제한되지만, 다른 NLP task에 대한 효과적인 adaptive CL방법론에 대한 추가 연구를 장려하고 보증한다. adaptive CL은 큰 데이터셋에 대해 learner model의 현 버전이 순위를 매길 때 훈련 중 여러 번 재연산이 필요하므로 연산량이 많이 필요한다. 저자들은 더 나아가 AbudctiveNLI와 같은 큰 데이터셋,과 UnifiedQA와 같은 큰 모델을 사용하여 CL을 최적화를 할 것이라 한다.

 

 

 

 

Conclusion

 

 저자들은 PTLMs를 사용한 다섯 개의 상식 추론에 대하여 adaptive CL과 fixed의 분석을 보여주었다. 결과에 따르면 CL은 PTML에 새로운 task를 도입할 때, prompt 조정 설정뿐만 아니라 fully-finetuned 에서 도메인 내 외부 데이터에 대해 downstream task 성능에 도움이 될 수 있음을 보여준다.