[2021] Robust Knowledge Graph Completion with Stacked Convolutions and a Student Re-Ranking Network
Justin Lovelace, Denis Newman-Griffis, Shikhar Vashishth, Jill Fain Lehman, Carolyn Penstein Rose´
본문의 논문은 ACL 2021 Accepted paper로, 여기를 확인해 주세요.
Abstract
NAACL 2022 paper을 보던 중 이와 연관된 논문이 있어 읽게 되었다. 전체적인 결과나 흐름을 꼼꼼히 보기보다는 모델 architecture과 train이 어떻게 진행되었는지만 간단히 요약해보려 한다.
Method
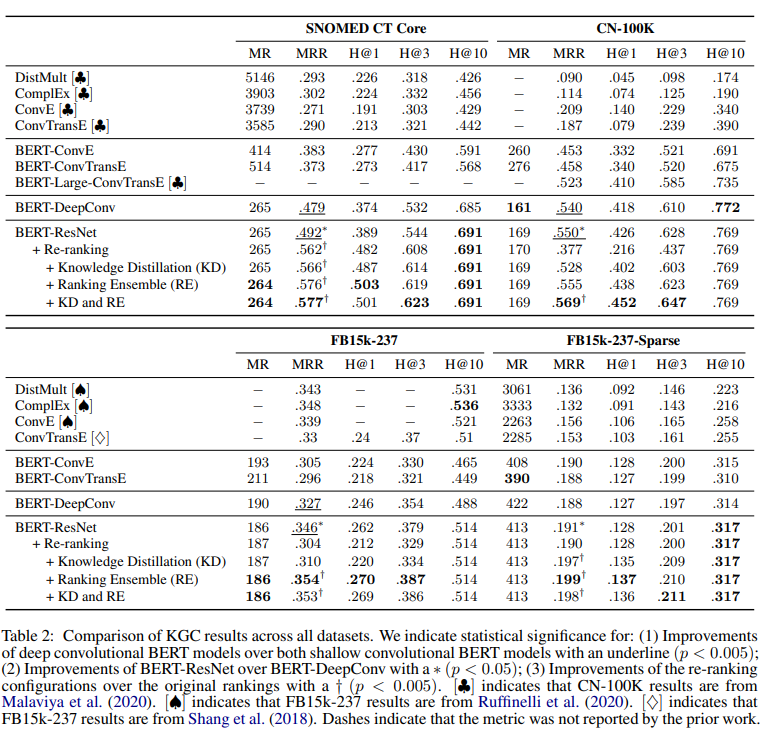
전반적으로 먼저 감을 잡아 보자면, 먼저 BERT에서 텍스트 entity embeddings를 develop하기 위해 feature 표현을 추출한다. 저자들은 자신들의 setting에서 기존의 neural KG architecture가 성능이 좋지 않음을 보고, deep convolutional vision 모델에서 혁신적인 구조를 활용한 deep convolutional network를 개발하였다. 이 모델은 downstream 성능 향상을 내는 훈련 데이터에서 복잡한 relationships에도 적합한 모델을 구상한 것이다.
마지막에는 이 ranking 모델 지식을 괜찮은 candidates의 순위를 조정하는 student re-ranking network로 distill한다. 그렇게 함으로써, KGC를 위한 re-ranking paradigm의 효과를 입증하고, 실제 KGs의 희소성에 대해 더 큰 견고성을 가진 KGC 파이프라인을 개발하였다.
1. Entity Ranking
저자들은 기존 KGC의 formulation을 따라 실험을 진행하였다. KG의 entity-relation-entity facts 인 $(e_1, r, e_2)$ 셋을 준비하고, entity fact가 없는 $(e_1, r, ?)$ 을 가지고 그래프에서 존재하는 모든 candidate entities $e_i$에 대한 점수를 계산한다. 당연히 효과적인 KGC 모델에서는 correct entity가 incorrect entity보다 점수가 높을 것이다. 이 모델에서는 forward와 inverse relations를 둘 다 고려한다. 예를 들면 treat와 treated by 를 둘 다 고려하는 것이다. inverse relations가 포함되지 않은 datasets에서는 모든 fact $(e_1, r, e_2) $에 대해 inverse fact $(e_2,r^{-1}, e_1)$를 도입한다.
- Textual Entity Representations
이제 여기서 BERT를 사용하여 KG의 연결성에 변함없는 entity embeddings를 만들어 낸다. CN-100K 와 FB15K-237 데이터 셋에는 BERT-base uncased 모델을 사용하고, SNOMED CT Core KG 데이터 셋에는 UMLS에서 생물학 용어에 적합한 PubMedBERT를 사용하였다.
BERT를 텍스트 entity 분별기로 사용하였고, concept name에 요약 feature 벡터를 얻기 위해 모든 BERT layer에서 token representations를 mean pool 하였다. 각각의 training examples에 수많은 잠재력 있는 candidate entities의 점수를 계산해야 하기 때문에 훈련 중에 이 embeddings를 고정하였다. 이로 인해 fine-tuning BERT의 연산량이 매우 커졌다.
- Deep Convolutional Architecture
computer vision에서 좋은 성능을 낸 ResNet을 사용한 knowledge base completion 모델을 만들었다. 여기서 ResNet architecture은 BERT features 공간과 relation embeddings 사이의 복잡한 interactions를 표현하기에 충분하였기에 사용하였다.
incomplete triple인 $(e_i, r_j, ?)$ 가 있을 때, 2개의 channels $\mathbf{q} \in \mathbb{R}^{2 \times d}$를 가진 길이 $d$의 feature vector를 만들기 위해 같은 차원 $\mathbf{r} \in \mathbb{R}^{1 \times d}$으로 학습된 relation embeddings로 사전에 계산된 entity embedding $\mathbf{e} \in \mathbb{R}^{1 \times d}$를 쌓아준다. 그런 다음 feature 벡터의 길이를 따라 너비 1의 커널을 가진 1차원 convolution을 적용하여 각 위치 $i$를 convolution이 $f \times f$ 필터를 갖는 2차원 공간 feature map $\mathbf{x}_i ∈ \mathbb{R}^{f \times f}$에 투영한다. 그러면 convolution은 $d$ channels를 가진 2차원의 공간 feature map인 $\mathbf{X} \in \mathbb{R}^{f \times f \times d}$를 만든다. 이는 incomplete한 query triple $(e_i, r_j, ?)$를 나타낸다.
공간 feature map인 $\mathbf{X}$ 는 측면 길이가 $f$ 와 $d$ channel인 사각형 이미지와 유사하여 ResNet과 같은 deep convoulutional 모델을 쉽게 적용할 수 있다. network의 깊이를 조절하는 N hyperparameter를 이용하여 공간 feature map으로 3N bottleneck blocks를 적용하였다. 여기서 bottleneck block은 3개의 convolutions를 연달아 붙인 모습으로, 1x1 convolution, 3x3 convolution, 1x1 convolution으로 구성된다. 첫 번째 1x1 convolution은 4개의 factor로 feature map 차원을 축소시키고, 두 번째 1x1 convolution은 feature map 차원을 저장한다. 이는 연산량이 큰 3x3 convolution의 차원을 줄이고 모델의 파라미터를 크게 증가시키지 않아도 이 모델의 깊이가 증가할 수 있다. 저자들은 bottleneck block의 feature 차원을 N에서 2N으로 증가시켜 마지막 feature map의 convolutions를 4$d$로 만들었다.
그리하여 deep networks에 training을 향상시키는 각 bottleneck block에 residual connection을 추가하였다. bottleneck block을 $\mathbf{F}(X)$라 하면, bottleneck block의 output은 $Y = \mathbf{F}(X) + X$가 된다. 각 convolutional layer 이전에 비선형 ReLU 를 적용하여 batch 일반화를 적용하였다.
3x3 convolutions 의 순환 padding을 사용하여 feature map의 공간적 크기를 유지하고, 모든 convolutions에 1 stride를 사용하였다. feature map의 더블 차원인 bottleneck block에는 residual connection을 위해 projection shorcut을 활용하였다.
- Entity Scoring
incomplete fact인 $(e_i, r_j, ?)$은 convolutional architecture에서 feature map $\mathbf{ \hat{X}} \in \mathbb{R}^{f \times f \times d}$를 만들어낸다. 요약 feature 벡터 $\mathbf{ \hat{x}} \in \mathbb{R}^{4d}$를 만들어 내는 공간 차원에서 average pooling을 한다. 그러고 원래의 embedding 차원인 $d$로 돌리기 위해 feature 벡터를 project 하는 비선형 PReLU를 사용한 fully connected layer를 적용한다. candidate entity embeddings가 있는 내적을 사용하여 candidate entities에 대한 최종 벡터 $\mathbf{ \hat{e}}$ 와 계산 점수를 나타낸다. 점수는 embedding matrix $y = \mathbf{ \hat{e}E} ^T$를 사용하여 모든 entities에 대해 효율적으로 계산할 수 있으며, 여기서 KG의 모든 $m$ entities에 대한 embeddings를 $\mathbf{E} \in \mathbb{R}^{m \times d}$ 로 저장한다.
2. Entity Re-Ranking
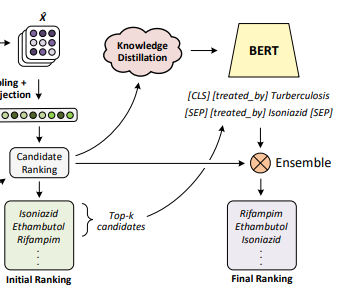
- Re-Ranking Network
모든 각 단계별 훈련 query에 대해 top-k 의 entities를 추출하는데 convolutional network를 사용하였고, 이 entities의 순위를 매기기 위해 re-ranking network를 train하였다. incomplete fact $(e_i, r_j ,?)$ 대신 full candidate fact $(e_i, r_j, e_k)$를 활용한 triplet 분류 모델로 논문의 student re-ranking network를 만들었다. 이는 network가 model의 모든 triplet 요소들 사이의 상호작용을 보기 때문이다. re-ranking setting은 직접적으로 fine-tuning BERT를 사용할 수 있게 한다.
knowledge graph에서 각 relation에 대한 relation tokens를 보여주고, head 와 tail entities에 relation tokens를 추가한 다음 둘을 연결한다. 그러면 triple ("head name", $r_i$, "tail name")은 "[CLS] [REL i] head name [SEP] [REL i] tail name [SEP]" 으로 나타난다.
- Knowledge Distillation
잘 만들어진 ranking model은 noisy training labels을 완화하는 데 사용되고 논문의 re-ranking 모델을 개선하는 데 사용할 수 있는 정보를 제공한다. training query $i$에 대해 논문의 teacher ranking model $f_T(\mathbf{x}_i)$를 사용하여 logits를 일반화한다. 여기서 k개의 candidate triples를 활용하면 teacher ranking model은 $f_T(\mathbf{x}_i)_{0:k}$로 다음과 같이 logits를 일반화한다.
$s_{ik:(i+1)k} = softmax(f_T(\mathbf{x}_i)_{0:k}/T)$, T : temperature
student model인 $f_S(x_i)$의 훈련 목적은 teacher에서 일반화한 logits $\mathbf{s}$와 noisy training labels $\mathbf{y}$를 사용한 이진 binary cross entropy $\mathcal{L}_{bce}$의 가중 평균을 구하는 것으로 다음과 같다.
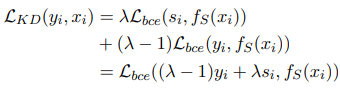
- Training
training set에서 모든 query에 대한 ranking 모델은 top $k$ = 10의 candidate를 추출하였다.
- Student-Teacher Ensemble
모든 query에서 상위 top $k$ = 10의 triples를 re-ranking network에 적용하였고 final ranking에서 teacher & student ensemble을 활용하였다. 그리하여 final ranking은 다음과 같이 계산되고, 0 ≤ $\alpha$ ≤ 1로 stuendt re-ranker의 영향을 조절한다.
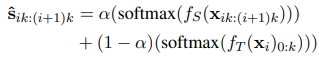
$\mathbf{ \hat{s}}_{ik:(i+1)k}$ 값은 무시할 만한 값이므로 0.01 단위로 [0,1]을 sweep하고 가장 좋은 평가 MRR값을 가지게 하는 $\alpha$ 를 택하였다.