[2019] Neo-GNNs: Neighborhood Overlap-aware Graph Neural Networks for Link Prediction
Seongjun Yun, Seoyoon Kim, Junhyun Lee, Jaewoo Kang∗ , Hyunwoo J. Kim*
본문의 논문은 여기를 확인해 주세요.
Abstract
GNN (Graph Neural Network)는 그래프 구조 데이터 학습을 위해 다양한 분야에서 많이 적용되었다. 노드 분류와 그래프 분류와 같은 전통적인 휴리스틱 방법 (경험 기반 방식)에서 큰 향상을 보여주었다. 하지만 GNN은 그래프 구조보다 매끄러운 노드 특성에 크게 의존하기 때문에, 구조적 정보, 예를 들어 오버랩된 이웃, degree, 최단 경로가 중요한 링크 예측에서 단순 휴리스틱보다 성능이 좋지 않았다. 이를 해결하기 위해 저자들은 인접 행렬에서 유용한 구조적 특성을 학습하고 링크 예측을 위해 겹쳐진 이웃을 추정하는 Neo-GNNs (Neighborhood Overlap-aware GNNs)을 제안한다. 이는 이웃 오버랩 기반의 휴리스틱 방법을 일반화하고 오버랩된 멀티 홉 이웃을 다룬다.
Introduction
그래프 기반 데이터는 소셜 네트워크 분석에서 생물학, 컴퓨터 비전 분야까지 다양한 분야에서 사용한다. 최근에는 GNN에서도 이 그래프 기반 데이터를 학습하는 방법을 많이 제안해오고 있다. GNN은 비선형 변환을 사용한 이웃으로부터 특성을 반복적으로 집계하여 그래프 또는 노드의 저 차원 표현을 학습한다. 그래서 이제껏 전통적인 방식인 휴리스틱 방법과 임베딩 기반 방법에서 상당한 성능을 보이고, 노드 분류와 그래프 분류, 그래프 생성과 같은 다양한 task에서 SOTA를 달성하였다.
하지만 링크 예측에서 전통적인 방식은 GNN과 비슷하거나 GNN이 더 뛰어난 성능을 보이고 있다. 이는 abstract에서 설명한 구조적 정보가 링크 예측에서 중요하기 때문이다. 최근엔 SEAL 이 타깃 노드 쌍과 그 이웃들 사이의 상대적 거리를 활용한 링크 예측을 위한 구조적 정보를 고려한 방법을 제안하였다. 그렇더라도 SEAL은 각 타겟 노드 쌍에 대해 추출된 subgraph에 GNN을 독립적으로 적용하기 위해 큰 연산량이 요구된다.
이런 한계점을 극복하기 위해 매뉴얼 한 과정 없이 링크와 관련된 주요 구조 정보를 고려하여 설계된 Neo-GNN을 제안하였다. 특히나 입력 노드의 사용 대신에, 이 방법은 인접 행렬에서 각 노드를 위해 유용한 구조적 특성을 생성하는 방법을 학습한다. Neo-GNN은 이웃 오버랩 인식 집합 스키마 (neighborhood overlap-aware aggregation scheme)를 통해 오버랩된 이웃의 구조적 특성을 고려함으로써 링크의 존재를 추정한다. 구조적 정보와 입력 노드의 특성 모두를 고려하기 위해 제안된 모델은 Neo-GNN과 기능 기반 GNN의 점수를 end-to-end 방식 (입력에서 출력까지 파이프라인 네트워크 없이 신경망으로 한 번에 처리)으로 적응적 결합한다.
저자들의 contributions을 정리하자면 다음과 같다.
① 인접 행렬에서 유용한 구조적 특성을 학습하는 Neo-GNNs를 제안하고, 링크 예측을 위해 오버랩된 이웃을 추정한다.
② Neo-GNNs는 오버랩 기반 휴리스틱 방법을 일반화하고 오버랩된 멀티홉 이웃을 다루었다.
③ OGB(Open Graph Benchmark datasets)에서 실험을 하였을 때, 링크 예측에서 SOTA를 달성함을 보인다.
≫ SEAL (논문: Link Prediction Based on Graph Neural Network) : GNN을 이용해 local subgraph로부터 휴리스틱을 배울 수 있는 방법을 제안한다.
Methods
방법론 설명에 앞서, 기본 notion을 먼저 정의하도록 하겠다.
1. Preliminaries
[Notions]
$N$개의 노드를 가진 무방향 그래프 $\mathcal{G = (V, E)}$ 는 노드의 셋인 $\mathcal{V}$ = {$v_1, v_2, ... ,v_N$} 와 엣지의 셋인 $\mathcal{E}$ = {$e_{ij} | v_i, v_j \in \mathcal{V}$} 로 구성되어 있다. 인접 행렬인 $A \in \mathbf{R}^{N \times N}$ 는 다음으로 정의된다.
$\begin{cases} A_{ij}=1,& e_{ij}∈\mathcal{E} \\A_{ij}=0, \mbox{ otherwise} \end{cases}$
차수 행렬인 $D \in \mathbf{R}^{N \times N}$ 은 $D_{ii} = \sum_{j} A_{ij}$ 로 정의된 대각 행렬이다. 그래프 $\mathcal{G}$ 의 노드들은 자신의 특성 벡터인 $x_i \in \mathbf{R}^F (i \in {1,2,...,N})$ 를 가지고, 행렬 형식에서 이런 벡터의 집합인 $X$는 $X \in \mathbf{N \times F}$ 로 정의 된다.
- Graph Neural Networks for Link Prediction
그래프 $\mathcal{G}$ 와 특성 행렬 $X$가 주어졌을 때, 신경망 그래프는 각 $l$-th GNN layer에 이웃 노드의 변형된 표현의 반복적인 집합에 의해 의미 있는 노드 표현을 다음과 같이 학습한다.
$H^{(l+1)} = \sigma(\tilde{A}_{GNN}H^{(l)}W^{(l)})$
- $\tilde{A}_{GNN} \in \mathbf{R}^{N \times N}$ : 각 GNN 구조에 따라 다른 방식으로 정규화된 인접 행렬 (e.g., \tilde{D}^{-1/2}(A+I)\tilde{D}^{-1/2})
- $W^{(l)} \in \mathbf{R} ^{d^{(l)} \times d^{(l+1)}}$ : 훈련 가능한 가중치 행렬
- $H^{(0)}$ : 노드 특성 행렬 $X \in \mathbf{R}^{N \times F}$
$L$ GNN layers를 쌓은 후, 노드 표현인 $H^{(L)}$ 은 각 링크 $(i,j)$ 를 예측하기 위해 사용된다 :
$\hat{y}_{i,j} = \sigma(s(h_i^{(L)}, h_j^{(L)}))$
- s(·,·) : 내적 연산 또는 MLP
- $h_i^{(L)}$ : $H^{(L)}$ 에서 노드 $i$의 표현
2. Neighborhood Overlap-based Heuristic Methods
휴리스틱 방법은 링크 예측에서 노드 쌍에 대해 구조적 정보 기반의 주어진 노드 쌍의 점수를 추정하는 방법이다. 앞서 말한 것처럼 비록 GNNs이 존재하는 전통적인 휴리스틱 방법보다 뛰어나긴 하지만, 링크 예측에서는 GNNs이 그래프 구조보다 완화된 노드 특성에 크게 의존하기 때문에 휴리스틱 방법이 GNNs와 비슷한 성능을 낸다. 특히나 이웃 오버랩 기반 휴리스틱 방법은 몇 가지 데이터 셋 (ogbl-collab and ogbl-ppa) 에서 GNNs보다 더 좋은 성능을 내기도 한다. 전형적인 이웃 오버랩기반 휴리스틱 방법은 Common Neighbor, RA (Resource Allocation), Adamic Adar이 있다. 여기서 Common Neighbor 은 노드 $u$ 와 $v$ 사이의 공통 이웃의 수에 의해 링크 $\mathcal{(u,v)}$ 의 점수를 측정하는 방법으로 다음과 같다.
$S_{CN}(u,v) = |\mathcal{N}(u) \cap \mathcal{N}(v)| = \sum_{k \in \mathcal{N}(u) \cap \mathcal{N}(v)} 1$
Common Neighbor 방법은 간단하고 효과적이지만, 각각의 공통 이웃의 중요성을 동등하게 평가하는 한계가 있다. 이를 해결하기 위해, 여러 휴리스틱 방법에서 RA와 Adamic-Adar 방법은 각 공통 이웃의 중요성을 고려하여 링크 점수를 추정한다. 낮은 차수의 이웃 노드가 더 중요하다는 직관에서 차수가 낮은 이웃에 더 가중치를 부여한다. 특히나 RA는 노드 $u,v$ 사이의 공통 이웃의 반대 차수의 수를 세어 링크 $(u,v)$ 의 점수 추정을 다음과 같이 한다.
$S_{RA}(u,v) = \sum_{k \in \mathcal{N}(u) \cap \mathcal{N}(v)} \frac{1}{d_k}$
- $d_k$ : 노드 $k$의 차수
Adamic-Adar는 노드 $u,v$ 사이의 공통 이웃 차수의 역 로그을 이용하여 RA에 비해 상대적으로 높은 차수에 대한 페널티가 감소된다. 이는 다음과 같다.
$S_{AA}(u,v) = \sum_{k \in \mathcal{N}(u) \cap \mathcal{N}(v)} \frac{1}{log d_k}$
위의 휴리스틱 방법들은 링크 예측에서 GNNs와 비슷한 성능을 보여준다. 그렇지만 이는 두 가지 한계점이 있다.
① 각 휴리스틱 방법은 이웃의 구조적 특성을 매뉴얼 하게, 즉 수동적으로 사용한다.
위의 예시에서 보면, 1, $\frac{1}{d}, \frac{1}{log d_k}$. 이는 각 데이터셋에서 도메인 전문가에게 가장 좋은 휴리스틱 방법을 수동적으로 선택해야 한다.
② 이는 구조적 유사성만을 고려한다는 점이다.
링크 예측에서 GNNs는 노드의 특징을 사용하는 것에 비해 그래프 구조를 잘 사용하지는 못하는 반면, 휴리스틱 방법은 노드의 특성을 잘 사용하지 못한다.
그래서 저자들은 위 둘의 한계점을 극복하기 위해 인접 행렬에서 유용한 구조적 특성을 학습하고, 오버랩된 이웃을 추정, end-to-end 방법으로 기존의 특성 기반 GNNs를 결합하는 Neo-GNN를 제안한다.
3. Neighborhood Overlap-aware Graph Neural Networks
Neo-GNNs 의 핵심 키가 두 가지 있다 :
(1) 구조적 특성 생성기 (2) 이웃 오버랩 인식 집계 스키마
첫 번째는 위 2-①번에서 언급한 부분으로, 구조적 특성을 학습하고 일반화하기 위해 그래프의 인접 행렬 $A \in \mathbf{R}^{N \times N}$ 만을 사용한 각 노드의 구조적 특성 생성을 학습하는 구조적 특성 생성기 함수인 $\mathcal{F}_{\theta}$ 를 아래와 같이 정의된다.
$ x_i^{struct} = \mathcal{F}_{\theta}(A_i) = f_{\theta_{node}} \left( \sum_{j \in \mathcal{N}_i} f_{\theta_{node}}(A_{ij}) \right) $
- $x_i^{struct}$ : 노드 $i$ 의 구조적 특성 값
- $\mathcal{F}_{\theta}$ : 학습 가능한 함수로, 두 MLP로 이루어져 있다. 각각은 노드와 엣지로 $f_{\theta_{node}}, f_{\theta_{edge}}$ 이다.
다시 말해, Neo-GNNs는 가장 좋은 구조적 특성을 생성하기 위해 입력으로 인접 행렬만을 사용한 것이다. 이 인접 행렬은 인접 행렬들의 거듭제곱 조합으로 대체될 수가 있다.
구조적 특성 생성기 함수인 $\mathcal{F}_{\theta}$ 는 각 휴리스틱 방법을 위한 구조적 특성을 생성한다. 예를 들면, $f_{\theta_{node}}$ 는 $f(x) = \frac{1}{log x}$ 의 역 로그 함수이고, $f_{\theta_{edge}}$는 항등함수인 $f(x) = x$ 이다. 그러면 $\mathcal{F}_{\theta}$는 Adamic-Adar 방법에서 사용된 특성과 같은 구조적 특성을 정확히 생성한다.
각 노드의 생성된 구조적 특성을 기반으로, 다음 단계는 주어진 노드들 사이에 오버랩된 이웃의 구조적 특성만을 고려한 유사성 점수를 계산한다. 기존의 GNNs는 두 가지 이유로 이 점수를 계산할 수 없는데, 바로 일반화된 인접 행렬과 노드의 수보다 숨겨진 표현의 낮은 차수 때문이다. 즉, $d << N$. 일반화된 인접 행렬은 GNNs가 이웃의 수를 못 세도록 하고, 낮은 차원은 이웃이 겹치는 것을 감지할 수 없는 집계 후에 각 이웃의 특징을 구별할 수 없게 만든다. 그래서 저자들은 이웃 오버랩 스코어를 계산하기 위해 이웃 오버랩 집계 스키마를 제안한다. 집계 후, 각 노드의 특성을 유지하기 위해, 구조적 특성 벡터 $x^{struct} \in \mathbf{R}^{N \times 1}$을 사용한 대각 행렬 $X^{struct} \in \mathbf{R}^{N \times N}$ 를 만든다. 여기서 사용한 대각 행렬은
$X^{struct} = diag(x^{struct})$
로 쓰인다.
그 후, 오버랩된 이웃의 수를 고려하기 위해, 비정규화된 인접 행렬 $A$를 곱함으로써 이웃의 특성을 계산한다. 여기서 행렬 $A$는 다음과 같다.
$Z = AX^{struct}$
$Z$ 의 각 $i$번째 행 벡터는 노드 $i$의 이웃하는 노드 각각을 모두 포함한다. 만약 $Z$에 두 행 벡터의 내적을 계산한다면, 오버랜된 이웃의 구조적 특성 값의 제곱과 같은 오버랩된 이웃만의 점수를 계산할 수 있다. 즉,
$z^T_i z_j = \sum_{k \in \mathcal{N}(i) \cap \mathcal{N}(j) } \left( x^{struct}_k \right)^2$
게다가, 오버랩된 이웃을 고려하기 위해 위의 식을 다음과 같은 멀티 홉으로 확장하였다.
$Z = g_{\Phi} \left( \sum_{l=1}^L \beta^{l-1}A^lX^{struct} \right)$
여기서 $\beta$ 는 가까운 이웃 vs 먼 이웃에 얼마나 많은 가중치가 주어지는지를 제어하는 하이퍼파라미터를 나타내며 $g_{Phi}$는 표현의 척도 $Z$를 컨트롤하는 MLP 이다. 노드 표현 $Z$가 구조적 정보에만 기반을 하기 때문에, 전통적인 특성 기반 GNNs를 사용한 특성 기반 노드 표현 $H \in \mathbf{R}^{N \times d'}$을 계산할 수 있다.
$H = GNN(X, \tilde{A}_{GNN}; W)$
여기서 $X \in \mathbf{R}^{N \times F}$는 raw 특성 행렬이고, $\tilde{A}_{GNN}$ 은 정규화된 인접 행렬, $W$는 GNN을 위한 파라미터이다. 주어진 링크 $(i,j)$를 가지고, Neo-GNNs는 각 표현 행렬 $Z$와 $H$ 둘의 유사성 점수를 계산하고, 훈련 가능한 파라미터인 $\alpha$로 두 점수의 convex 결합을 계산한다.
$\hat{y}_{ij} = \alpha · \sigma(z^T_i z_j) + (1 - \alpha) · \sigma(s(h_i, h_j))$
다음의 식을 기반으로, 각각의 모델을 세 개의 기본 cross entropy (이진 cross entropy) 를 사용하여 저자들의 모델을 훈련시킨다.
$\mathcal{L} = \sum_{(i,j) \in D} (\lambda_1BCE(\hat{y}_{i,j}, y_{i,j}) + (\lambda_2BCE(\sigma(z^T_i z_j), y_{i,j}) + (\lambda_3BCE(\sigma(s(h_i, h_j)), y_{i,j}) )$
BCE(·,·)는 binary cross entropy 이고, $\lambda_i$는 가중치이다.
Experiments
- Datasets
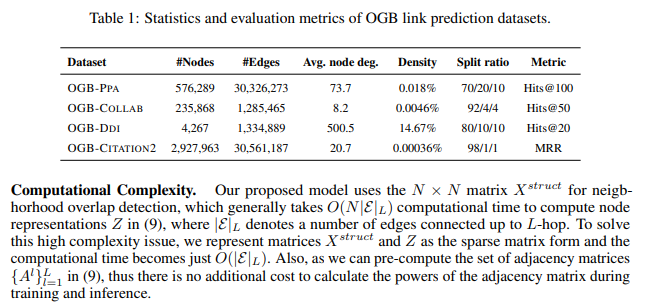
- Results on Link Prediction
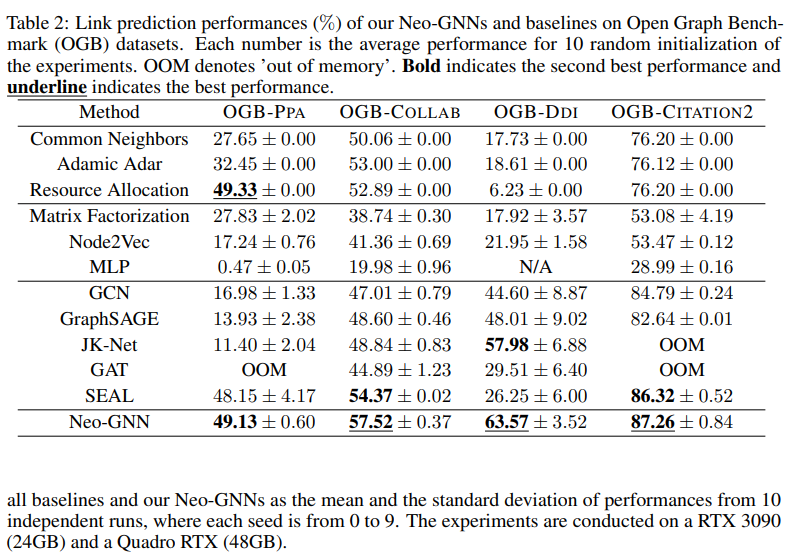
Conclusion
본 논문에서 다룬 Ablation study는 생략하였다. 궁금한 분들은 직접 논문을 읽어보길 추천한다.
저자들은 링크 예측에서 핵심 요소가 될 구조적 정보를 활용하고 학습한 Neo-GNNs를 소개한다. 유용한 구조적 특성을 인접 행렬에서 가져와 학습하고, 링크 예측을 위해 오버랩된 이웃을 측정하였다. 또한 특성 기반 GNN과 Neo-GNN을 적응적으로 결합하여 구조적 특성과 입력 노드 특성 모두 고려하였다. 게다가, Neo-GNN은 여러 이웃 오버랩 기반 휴리스틱 방법을 일반화하였고, 오버랩된 멀티 홉 이웃을 다루었다. 네 개의 Open Graph Benchmark (OGB) 데이터 셋에서 링크 예측에서는 SOTA를 달성하였다.
향후, 저자들은 Neo-GNN을 더 일반화하고, 효율적인 희소 행렬 연산으로 확장할 예정이다.