[2022] Learning Inter-Entity Interaction for Few-Shot Knowledge Graph Completion
Yuling Li, Kui Yu∗ , Xiaoling Huang, Yuhong Zhang
본문의 논문은 EMNLP 2022 Accepted paper로, 여기를 확인해 주세요.
Abstract
Few-shot knowledge graph completion (FKGC) 은 few-shot을 이용해 추론한 entity 쌍을 사용하여 알려지지 않은 relation의 triples를 발견하는 것이 목적인 그래프이다. 최근 이 연구에는 head와 tail entities의 neighborhoods를 따로 encoding 하여 entity 쌍의 의미론적인 표현을 학습하는 데에 집중되어 있었다. 하지만 앞선 방법은 entity 간의 상호작용을 무시하여, 특히 이런 entity 쌍이 1-to-N, N-to-1, N-to-N 관계와 연관된 경우에 entity 쌍에 대한 표현의 차별성이 낮게 보이게 된다.
그래서 저자들은 head와 tail entities의 내부적인 entity 상호 작용성을 고려한 새로운 FKGC 모델인, Cross-Interaction Attention Network(CIAN)을 발표하였다. 본 모델은 먼저 task relation과 각 entity neighbor 간의 attention을 계산하여 entities내에 상호 작용을 확인한 후, entity가 쌍을 이룬 entities의 neightborhood에 attention을 주도록 하여 head와 tail entities 간의 상호 작용을 모델링한다. 이로 인해 CIAN은 head와 tail entities 간의 연관 있는 의미를 찾아내고, entity 쌍 표현에서 더 차별성을 만들어 냈다.
Introduction
이 전에는 KGE (Knowledge Graph Embeddings)에 관한 논문을 보았는데, SOTA를 달성한 KGC 모델은 종종 KGE를 기반으로 한 모델들이다. KGE의 핵심은, entities와 relations를 낮은 차원의 벡터 공간으로 embeddings 하고 그 embeddings를 기반으로 triples가 잘 link 되고 완벽한지 평가하는 것이다. 이런 성공적인 부분에도 불구하고, KGE 기반 모델들은 모든 relations에 대해 triples가 충분히 훈련이 돼야 한다는 것이다. 하지만 많은 데이터가 대부분 그렇게 완전한 triple의 형태를 가지고 있지 않은 점이 KGE의 한계이다.
FKGC는
결론적으로, 생성된 entity 쌍들은 큰 차별성이 없다는 것, 특히 다양한 다른 entity 쌍들이 공통의 entities를 포함하는 1-to-N, N-to-1, N-to-N 에서 그렇다.
그리하여 저자들은 head와 tail entity의 내부적인 상호작용을 고려할 수 있는, 이 두 entities 사이에 의미론적으로 상관있는 attributes에 attention을 더 주어 중요성을 보이도록 했다.

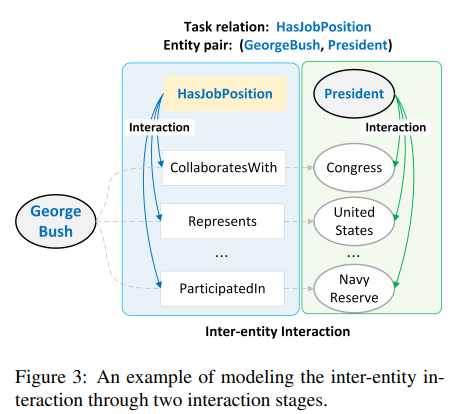
위 figure로 간단히 설명하자면, George Bush는 HasJobPosition 에서 두 가지 entity를 가진다. 보통 우리가 알아보기엔 President, 즉 파란색 쪽에 대해 설명을 보면 될 것이고, 군인들에게는 Pilot, 즉 녹색 부분을 보면 더 이해를 쉽게 할 수도 있다.
이 처럼 두 entities를 모두 포함하여 캐릭터를 더 잘 설명할 수 있도록 하였다.
Related Work
모든 관련 연구를 알아보기보다는, 뒤에 실험에서 사용된 baseline 중심으로 보도록 하겠다.
FKGC는 두 가지 메인 카테고리로 나눌 수 있다.
- Metric 학습 기반 방법
① GMatching은 one-shot KG completion을 해결하기 위한 첫 번째 연구이다. 이 방법은 직접적인 neighbors를 encoding하여 entity를 embedding 하고 여러 단계의 matching 과정을 거쳐 query와 추론된 entity 쌍 사이의 유사성을 측정한다.
② FSRL은 회귀 autoencoder aggregation network를 통한 few-shot 방법으로 GMatching을 확장시킨 버전이고 entitiy embeddings의 질을 향상시키기 위해 이질적인 neighbor encoder를 사용하였다.
③ 다양한 triples에서 같은 entity를 구분하는 학습을 위한 위 두 방법과는 다르게, FAAN은 다른 task relations에서 entities의 동적인 특성을 확인하고, task 인식 entity 표현을 학습하였다.
④P-INT는 entity 쌍을 표현하기 위해 head에서 tail entities의 경로를 활용하고 support 와 query entity 쌍들 사이의 경로 상호 작용을 계산하였다.
- Meta 학습자 기반 방법
① MetaR은 head와 tail entities의 embeddings를 사용한 relation 특화 meta정보를 생성하고 gradient meta를 통해 relation meta를 업데이트한다.
② GANA는 entities의 neighbor 정보를 통합하여 relation-meta를 학습하고, 모델의 복잡한 relations를 위해 meta학습 기반 TransH 모듈을 사용하였다.
Problem Formulatoin
FKGC 의 기본적인 setting에 따라,
few-shot 학습을 위해 실제 테스트 상황을 비슷하게 만든 일시적인 과정을 적용한다. 특히나 meta 훈련의 반복은,
저자들은
★ 여기서 잠깐 few-shot KG completion의 정의를 보자면,
- task relation
Methodology

CIAN은 대략적으로 다음과 같은 구조를 지니고, 다음 과정들을 거친다.
1. Modeling the Inter-entity Interaction
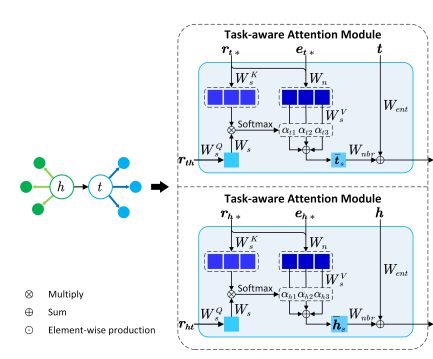
이 부분에서는 head와 tail entities의 내부적인 entity의 상호작용을 보고 상응하는 entity쌍들의 표현을 위한 관계있는 의미들을 활용할 것이다. 첫 번째로, task-aware attention module에서 각 entity에 task 관련 의미 attributes를 추출한다. 이는 FAAN에서 영감을 얻은 구조인데, entites가 task relations에 적용된 의미 attributes를 보여준다. task 관련 attributes의 기반은, head와 tail entities 사이의 관련 있는 의미 attributes를 찾아내는 것이다. 이는 entity-pair-aware attention module에서 고안한 방법으로, 하나의 entity와 그 entity쌍의 neighbors 사이의 상호 작용의 attention을 계산하는 시도를 하였다.
- Task-aware Attention Module
task relation
타깃으로 head entity
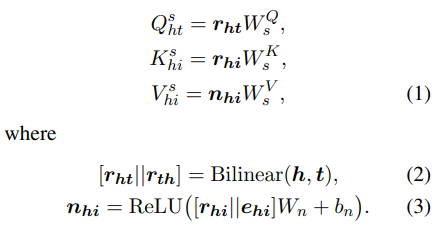
여기서
그리고 이제 bilinear 내적으로 neighboring relation과 task relation 사이의 상관성을 계산하고 softmax를 사용하여 모든 neighbors의 관련성을 다음과 같이 일반화한다.
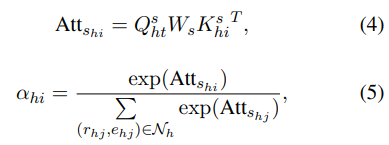
여기서 사용한
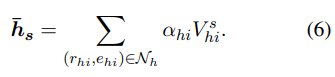
이 방법에서, task relation과 더 관련 있는 entity neighbors는 더 큰 가중치를 부여받게 되며, 이는 더 가치 있는 이웃 정보를 발견하게 된다.
이제 마지막으로, task-aware entity representation을 만들기 위해 가중치 neighbor 표현
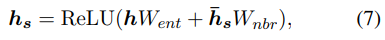
위의 두 $W_{ent}, W_{nbr} \in \mathbb{R}^{d times d}$는 훈련 가능한 가중치 벡터이다.
위의 과정을 똑같이 tail entity
- Entity-pair-aware Attention Module
entity-pair-aware attention module에서는 한 쌍의 entities가 주어질 때, 어떤 한 entity가 그 entity 쌍의 각 이웃을 가져오게 하여 head 와 tail entities 사이의 관련 있는 의미적 유사성을 알아내는 것이 목표이다. 여기서 생성된 entity-pair-aware 표현들은 entity 쌍에 상응하는 의미적 표현을 쌍으로 함께 형성하게 된다. 아래에서 수식과 함께 상세한 과정을 보도록 하겠다.
head entity를 target으로 잡고, entity-pair-aware attention module에

이후,

그런 다음, entity-pair-aware neighbor 표현인

(10)의 베타 값이 높게 나올 수록 h와 entity 쌍
이 과정을 모두 거치면
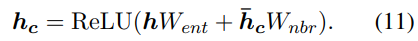
위 과정과 비슷하게 tail entity
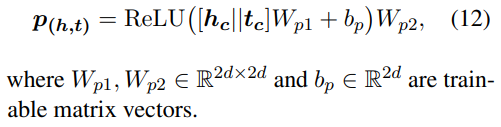
2. Matching Support and Query Sets
다음 과정에서는 entity 쌍에서 생성된 의미적 표현을 바탕으로, support set에서 entity 쌍의 reference 표현으로부터 일반적인 표현, 다시 말해, few-shot relation의 prototype을 학습할 것이다. tiples의 reference가 적기 때문에 벡터 공간에서 한 reference triple이 다른 references에서 멀다면, 이것은 상응하는 prototype에서 큰 편차를 가져올 것이다. 그러므로 더 정보력있는 references를 선택하기 위해 attention mechanism을 선보이고 훈련 동안 noisy references를 제거한다.
자세하게 보자면, query set
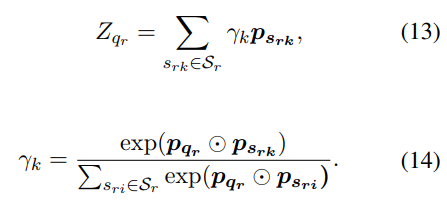
여기서
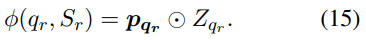
3. Loss Function and Model Training
task
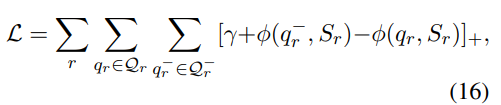
Experiments
- Datasets

위 두 데이터셋은 500개가 조금 안되는 relations이지만 50개보다 많은 triples를 가지고 있는 few-shot relations이다. 각각의 데이터셋은 training/test/validation은 대략 10:2:1 정도의 비율로 사용하였다.
- Comparisons

전반적으로 저자들이 제안한 CIAN이 가장 좋은 결과를 내고 있음을 볼 수 있고, 아래의 표는 K개의 few-shot size 별 baseline과 CIAN의 모델 성능 비교이다.

전반적으로 FKGC의 모든 모델이 size가 커질수록 꾸준한 향상을 보이는 것은 아니지만, 상대적으로 CIAN은 안정적으로 성능이 향상함을 보이고 있다.

위는 full model의 성능, 그 아래로 task-aware attention module을 제거했을 때, entity-pair-aware attention module을 제거했을 때, 마지막으로 task-aware attention module에서 아래의 bilinear 함수를 적용하지 않았을 때의 성능 비교이다.

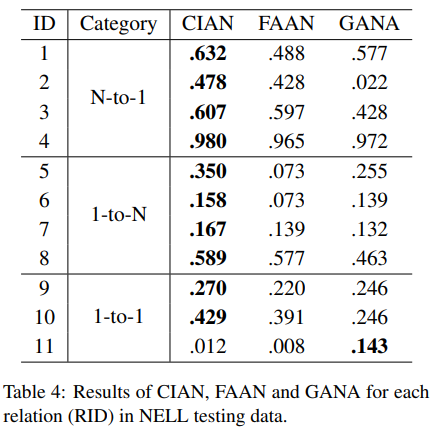
NELL testing data 에서 baseline과 비교하였을 때, CIAN은 전체적으로 가장 좋은 성능을 보이며, 이는 entity 쌍의 표현을 위한 head와 tail entities 사이의 상대적인 의미론 활용에서 더 복잡한 relations에 도움이 됨을 보이고 있다.
그리고 아래는 2D를 이용한 embedding 시각화를 나타내었는데, 저자들의 모델이 positive 와 negative를 잘 구분함을 보이고 있다.
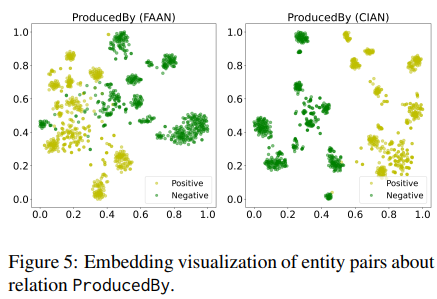
Conclusion
다시 정리하자면, 본 논문은 few-shot KG completion을 위해 inter-entity- inter-action을 사용하고 cross-interaction attention network를 제안하였다. 특히나 task-aware attention module은 task와 관련 있는 entity attributes를 추출하기 위한 방법이고, entity-pair-aware attention module은 head와 tail entities 사이의 의미적으로 관련 있는 attributes를 식별한다. 또한 이 결과는 기존 baseline보다 더 좋은 성능을 내어 SOTA를 달성함을 보인다. 더 나아가 few-shot KG completion을 해결하기 위해 entities의 문법적인 표현과 같은 side 정보를 어떻게 다룰지 알아볼 예정이다.
한계점으로 볼 부분은,
① 저자들의 모델이 direct neighbors가 적은, 많은 long-tailed entities에 대해서는 성능이 낮아짐을 볼 수 있었다. 이는 희소한 neighbors가 모델의 inter-entity interaction에서 이점을 주지 않기 때문이다.
② 저자들의 모델이 entity neighborhoods 사이의 상호 작용을 이용하는데에 초점이 맞추어져 있기 때문에, background graph가 entities의 neighbors를 제공하기 위해 필요하다.